5. 최적화와 시각화

“이론과 실제 사이에는 이론과 실제의 차이보다 더 큰 차이가 있다.” - 얀 르쿤 (Yann LeCun), 2018 튜링상 수상자

딥러닝 모델의 성공은 효과적인 최적화 알고리즘과 적절한 가중치 초기화 전략에 크게 의존합니다. 이 장에서는 딥러닝 모델 학습의 핵심 요소인 최적화와 초기화 방법을 심층적으로 탐구하고, 이 과정을 시각화를 통해 직관적으로 이해하는 방법을 제시합니다. 먼저, 신경망 학습의 초석이 되는 다양한 가중치 초기화 방법의 발전 과정과 그 수학적 원리를 살펴봅니다. 그런 다음, 경사하강법(Gradient Descent)을 시작으로, Adam, Lion, Sophia, AdaFactor 등 최신 최적화 알고리즘의 작동 원리와 성능을 비교 분석합니다. 특히, 이론적인 배경뿐만 아니라, 실제 딥러닝 모델 학습 과정에서 각 알고리즘이 어떻게 동작하는지 실험을 통해 확인합니다. 마지막으로, 고차원 손실 함수 공간(loss landscape)을 시각화하고 분석하는 다양한 기법들을 소개하고, 이를 통해 딥러닝 모델의 학습 동역학(learning dynamics)을 이해하는 심층적인 통찰력을 제공합니다.

5.1 파라미터 초기화의 발전과 현대적 접근

신경망의 파라미터 초기화는 모델의 수렴성, 학습 효율성, 그리고 최종 성능을 결정짓는 핵심 요소 중 하나입니다. 잘못된 초기화는 학습 실패의 주 원인이 될 수 있습니다. 파이토치(PyTorch)는 torch.nn.init 모듈을 통해 다양한 초기화 방법을 제공하며, 자세한 내용은 공식 문서에서](https://www.google.com/search?q=https://pytorch.org/docs/stable/nn.init.html)%EC%97%90%EC%84%9C%EC%97%90%EC%84%9C)) 확인할 수 있습니다. 초기화 방법의 발전 과정은 딥러닝 연구자들이 신경망 학습의 어려움을 극복해 온 역사를 반영합니다. 특히, 부적절한 초기화는 그래디언트 소실(vanishing gradient)이나 폭발(exploding gradient) 현상을 유발하여, 심층 신경망의 학습을 방해하는 주범으로 지목되었습니다. 최근에는 GPT-3, LaMDA와 같은 대규모 언어 모델(Large Language Models, LLMs)의 등장으로 초기화의 중요성이 더욱 강조되고 있습니다. 모델의 규모가 커질수록, 초기 파라미터의 분포가 학습 초기 단계에 미치는 영향이 증폭되기 때문입니다. 따라서, 모델의 특성과 규모에 맞는 적절한 초기화 전략을 선택하는 것이 딥러닝 모델 개발의 필수적인 단계가 되었습니다.

5.1.1 초기화 방법의 수학적 원리

신경망 초기화 방법의 발전은 깊이 있는 수학적 이론과 수많은 실험적 검증이 함께 이루어진 결과입니다. 각 초기화 방법은 특정한 문제 상황(예: 특정 활성화 함수의 사용, 네트워크의 깊이, 모델의 종류)을 해결하거나, 학습 동역학(learning dynamics)을 개선하기 위해 고안되었으며, 시대의 흐름에 따라 새로운 도전 과제에 대응하며 발전해 왔습니다.

다음은 이 책에서 중점적으로 비교하고 분석할 초기화 방법들입니다. (전체 구현 코드는 chapter_04/initialization/base.py 파일에 수록되어 있습니다.)

Code

!pip install dldna[colab] # in Colab
# !pip install dldna[all] # in your local

%load_ext autoreload
%autoreload 2

Code

import torch
import torch.nn as nn
import numpy as np

# Set seed
np.random.seed(7)
torch.manual_seed(7)


from dldna.chapter_05.initialization.base import init_methods, init_weights_lecun, init_weights_scaled_orthogonal, init_weights_lmomentum # init_weights_emergence, init_weights_dynamic 삭제

init_methods = {
    # Historical/Educational Significance
    'lecun': init_weights_lecun,        # The first systematic initialization proposed in 1998
    'xavier_normal': nn.init.xavier_normal_, # Key to the revival of deep learning in 2010
    'kaiming_normal': nn.init.kaiming_normal_, # Standard for the ReLU era, 2015

    # Modern Standard
    'orthogonal': nn.init.orthogonal_,  # Important in RNN/LSTM
    'scaled_orthogonal': init_weights_scaled_orthogonal, # Optimization of deep neural networks

    # 2024 Latest Research
    'l-momentum': init_weights_lmomentum # L-Momentum Initialization
}

전통적 초기화

LeCun 초기화 (1998년): \(std = \sqrt{\frac{1}{n_{in}}}\)
- Yann LeCun이 1998년에 제안한 방법으로, 입력 차원(\(n_{in}\))만을 고려하여 가중치의 표준편차를 결정합니다. 각 뉴런의 출력이 입력 개수에 따라 크게 변하는 것을 방지하고자 했으나, 깊은 네트워크에서는 층이 깊어질수록 활성화 값의 분산이 감소하는 경향이 있었습니다. 이는 특히 tanh와 같은 시그모이드 계열 활성화 함수를 사용할 때 두드러졌습니다.

현대적 초기화

Xavier 초기화 (Glorot, 2010): \(std = \sqrt{\frac{2}{n_{in} + n_{out}}}\)
- Xavier Glorot와 Yoshua Bengio가 제안한 방법으로, 입력(\(n_{in}\))과 출력(\(n_{out}\)) 차원을 모두 고려하여 그래디언트 소실/폭발 문제를 완화했습니다. 핵심은 각 층의 활성화 값과 그래디언트의 분산을 적절하게 유지하는 것입니다. 주로 sigmoid, tanh와 같은 포화형(saturating) 활성화 함수와 함께 사용될 때 효과적입니다.
Kaiming 초기화 (He, 2015): \(std = \sqrt{\frac{2}{n_{in}}}\)
- Kaiming He 등이 제안한 방법으로, ReLU 활성화 함수의 특성(음수 입력을 0으로 만듦)을 고려하여 설계되었습니다. ReLU는 활성화 값의 분산을 절반으로 줄이는 경향이 있어, 이를 보상하기 위해 Xavier 초기화보다 큰 분산(\(\sqrt{2}\) 배)을 사용합니다. 이는 “죽은 뉴런(dead neuron)” 문제를 줄이고 깊은 네트워크에서도 안정적인 학습을 가능하게 하여, 현재 ReLU 계열 활성화 함수 사용 시 사실상의 표준(de facto standard)이 되었습니다.

수학적 원리

대부분의 현대적 초기화 방법은 다음 세 가지 핵심 원리를 (명시적 또는 암묵적으로) 따릅니다.

분산 보존 (Variance Preservation): 순전파 시 활성화 값의 분산과 역전파 시 그래디언트의 분산이 층별로 일정하게 유지되어야 합니다.

\(Var(y) \approx Var(x)\)

이는 신호가 너무 커지거나 작아지지 않도록 하여 안정적인 학습을 돕습니다.
스펙트럴 제어 (Spectral Control): 가중치 행렬의 특이값(singular value) 분포를 제어하여, 학습 과정의 수치적 안정성을 확보해야 합니다.

\(\sigma_{max}(W) / \sigma_{min}(W) \leq C\)

이는 특히, 순환 신경망(RNN)과 같이 가중치 행렬이 반복적으로 곱해지는 구조에서 중요합니다.
표현력 최적화 (Expressivity Optimization): 가중치 행렬의 유효 랭크(effective rank)를 최대화하여, 네트워크가 충분한 표현력을 갖도록 해야 합니다.

\(rank_{eff}(W) = \frac{\sum_i \sigma_i}{\max_i \sigma_i}\) 최근 연구들은 이러한 원리들을 명시적으로 만족시키기 위해 노력하고 있습니다.

결론적으로, 초기화 방법은 모델의 규모, 구조, 활성화 함수, 그리고 최적화 알고리즘과의 상호작용을 고려하여 신중하게 선택해야 합니다. 이는 모델의 학습 속도, 안정성, 그리고 최종 성능에 큰 영향을 미치기 때문입니다.

클릭하여 내용 보기 (딥다이브: 심층 신경망 초기화의 수학적 원리와 최신 기법)

심층 신경망 초기화의 수학적 원리와 최신 기법

1. 분산 보존 원리 (Variance Preservation Principle)

1.1 이론적 기반

신경망의 깊이가 증가함에 따라 순전파(forward propagation) 및 역전파(backpropagation) 과정에서 신호의 통계적 특성(특히 분산)을 보존하는 것은 매우 중요합니다. 이는 신호가 소실(vanishing)되거나 폭발(exploding)하는 것을 방지하여 안정적인 학습을 가능하게 합니다.

\(l\)번째 층의 활성화 값을 \(h_l\), 가중치 행렬을 \(W_l\), 편향을 \(b_l\), 활성화 함수를 \(f\)라고 할 때, 순전파는 다음과 같이 표현됩니다.

\(h_l = f(W_l h_{l-1} + b_l)\)

입력 신호 \(h_{l-1} \in \mathbb{R}^{n_{in}}\)의 각 요소가 평균 0, 분산 \(\sigma^2_{h_{l-1}}\)을 갖는 독립적인 확률변수이고, 가중치 행렬 \(W_l \in \mathbb{R}^{n_{out} \times n_{in}}\)의 각 요소가 평균 0, 분산 \(Var(W_l)\)을 갖는 독립적인 확률변수이며, 편향 \(b_l = 0\)이라고 가정하면, 활성화 함수가 선형이라고 가정할 때 다음이 성립합니다.

\(Var(h_l) = n_{in} Var(W_l) Var(h_{l-1})\) (단, \(n_{in}\)은 \(l\)번째 층의 입력 차원)

활성화 값의 분산이 보존되려면, \(Var(h_l) = Var(h_{l-1})\) 이어야 하므로, \(Var(W_l) = 1/n_{in}\) 이어야 합니다.

역전파 시에는, 오차 신호 \(\delta_l = \frac{\partial L}{\partial h_l}\) (단, \(L\)은 손실 함수)에 대해 다음과 같은 관계가 성립합니다.

\(\delta_{l-1} = W_l^T \delta_l\) (활성화 함수가 선형이라고 가정)

따라서, 역전파 시 분산 보존을 위해서는 \(Var(\delta_{l-1}) = n_{out}Var(W_l)Var(\delta_l)\) 이므로, \(Var(W_l) = 1/n_{out}\) 이어야 합니다. (단, \(n_{out}\)은 \(l\)번째 층의 출력 차원)

1.2 비선형 활성화 함수 확장

ReLU 활성화 함수

ReLU 함수 (\(f(x) = max(0, x)\))는 입력의 절반을 0으로 만들기 때문에 활성화 값의 분산이 줄어드는 경향이 있습니다. Kaiming He는 이를 보정하기 위해 다음과 같은 분산 보존 식을 제안했습니다.

\(Var(W_l) = \frac{2}{n_{in}} \quad (\text{ReLU 특화})\)

이는 ReLU를 통과하면서 발생하는 분산 감소를 2배 증가시켜 보상하는 것입니다.

Leaky ReLU 활성화 함수

Leaky ReLU (\(f(x) = max(\alpha x, x)\), \(\alpha\)는 작은 상수)의 경우, 일반화된 공식은 다음과 같습니다.

\(Var(W_l) = \frac{2}{(1 + \alpha^2) n_{in}}\)

1.3 확률론적 접근 (참고)

Fisher Information Matrix (FIM)의 역행렬을 사용하여 초기화하는 방법도 있습니다. FIM은 파라미터 공간에서의 곡률 정보를 담고 있어, 이를 활용하면 더 효율적인 초기화가 가능합니다. (더 자세한 내용은 참고 문헌 [4] Martens, 2020 참조).

2. 스펙트럴 제어 (Spectral Control)

2.1 특이값 분해와 학습 역학

가중치 행렬 \(W \in \mathbb{R}^{m \times n}\)의 특이값 분해(Singular Value Decomposition, SVD)는 \(W = U\Sigma V^T\) 로 표현됩니다. 여기서 \(\Sigma\)는 대각 행렬이며, 대각 성분은 \(W\)의 특이값 (\(\sigma_1 \geq \sigma_2 \geq ... \geq 0\))입니다. 가중치 행렬의 최대 특이값(\(\sigma_{max}\))이 너무 크면 그래디언트 폭발(exploding gradient)을, 최소 특이값(\(\sigma_{min}\))이 너무 작으면 그래디언트 소실(vanishing gradient)을 유발할 수 있습니다.

따라서, 특이값의 비율(조건수, condition number) \(\kappa = \sigma_{max}/\sigma_{min}\) 을 제어하는 것이 중요합니다. \(\kappa\)가 1에 가까울수록 안정적인 그래디언트 흐름이 보장됩니다.

Theorem 2.1 (Saxe et al., 2014): 직교 초기화(orthogonal initialization)된 심층 선형 신경망에서 각 층의 가중치 행렬 \(W_l\)이 직교 행렬이면, 입력에 대한 출력의 야코비안 행렬(Jacobian matrix) \(J\)의 Frobenius norm은 1로 유지됩니다.

\(||J||_F = 1\)

이는 매우 깊은 네트워크에서도 그래디언트 소실 또는 폭발 문제를 완화하는 데 도움이 됩니다.

2.2 동적 스펙트럴 정규화

Miyato et al.(2018)은 GAN 학습의 안정성을 높이기 위해 가중치 행렬의 스펙트럴 노름(spectral norm, 최대 특이값)을 제한하는 Spectral Normalization 기법을 제안했습니다.

\(W_{SN} = \frac{W}{\sigma_{max}(W)}\)

이 방식은 GAN 학습에서 특히 효과적이며, 최근에는 Vision Transformer 등 다른 모델에도 적용되고 있습니다.

3. 표현력 최적화 (Expressivity Optimization)

3.1 유효 랭크 이론

가중치 행렬 \(W\)가 얼마나 다양한 특징(feature)을 표현할 수 있는지는 특이값 분포의 균일성으로 측정할 수 있습니다. 유효 랭크(effective rank)는 다음과 같이 정의됩니다.

\(\text{rank}_{eff}(W) = \exp\left( -\sum_{i=1}^r p_i \ln p_i \right) \quad \text{where } p_i = \frac{\sigma_i}{\sum_j \sigma_j}\)

여기서 \(r\)은 \(W\)의 랭크, \(\sigma_i\)는 \(i\)번째 특이값, \(p_i\)는 정규화된 특이값입니다. 유효 랭크는 특이값의 분포를 나타내는 지표로, 값이 클수록 특이값이 균등하게 분포되어 있음을 의미하며, 이는 곧 높은 표현력을 나타냅니다.

3.2 초기화 전략 비교표

초기화 방법	특이값 분포	유효 랭크	적합 아키텍처
Xavier	비교적 빠르게 감소	낮음	얕은 MLP
Kaiming	ReLU 활성화 함수에 맞게 조정 (상대적으로 덜 감소)	중간	CNN
Orthogonal	모든 특이값이 1로 동일	최고	RNN/Transformer
Emergence-Promoting	네트워크 크기에 따라 조정, 상대적으로 완만하게 감소 (heavy-tailed distribution에 가까움)	높음	LLM

3.3 Emergence-Promoting 초기화

Emergence-Promoting 초기화는 대규모 언어 모델(LLM)에서 창발적 능력(emergent abilities)을 촉진하기 위해 제안된 최신 기법입니다. 이 방법은 네트워크의 크기(특히 층의 깊이)에 따라 초기 가중치의 분산을 조정하여, 유효 랭크를 증가시키는 효과를 냅니다.

Chen et al. (2023)은 Transformer 모델에서 다음과 같은 scaling factor \(\nu_l\)를 제안했습니다.

\(\nu_l = \frac{1}{\sqrt{d_{in}}} \left( 1 + \frac{\ln l}{\ln d} \right)\)

여기서 \(d_{in}\)은 입력 차원, \(l\)은 층의 인덱스, \(d\)는 모델의 깊이입니다. 이 scaling factor를 가중치 행렬의 표준 편차에 곱하여 초기화합니다. 즉, \(\nu_l\) 를 곱한 \(\sqrt{2/n_{in}}\)를 표준편차로 하는 정규분포에서 샘플링합니다.

4. 초기화와 최적화의 상호작용

4.1 NTK 이론 확장

Jacot et al.(2018)의 Neural Tangent Kernel (NTK) 이론은 “매우 넓은”(infinitely wide) 신경망의 학습 동역학을 분석하는 데 유용한 도구입니다. NTK 이론에 따르면, 초기화 시점에서 매우 넓은 신경망의 헤시안 행렬의 기댓값은 identity matrix에 비례합니다. 즉,

\(\lim_{n_{in} \to \infty} \mathbb{E}[\nabla^2 \mathcal{L}] \propto I\) (초기화 시점에서)

이는 Xavier 초기화가 넓은 신경망에서 최적에 가까운 초기화를 제공한다는 것을 시사합니다.

4.2 메타 초기화 전략

MetaInit (2023)과 같은 최근 연구에서는 메타러닝을 통해 주어진 아키텍처와 데이터셋에 맞는 최적의 초기화 분포를 학습하는 방법을 제안합니다.

\(\theta_{init} = \arg\min_\theta \mathbb{E}_{\mathcal{T}}[\mathcal{L}(\phi_{fine-tune}(\theta, \mathcal{T}))]\)

여기서 \(\theta\)는 초기화 파라미터, \(\mathcal{T}\)는 학습 task, \(\phi\)는 \(\theta\)로 초기화된 모델을 fine-tuning하는 과정을 나타냅니다.

5. (참고) 물리 기반 초기화 기법

최근에는 물리학의 원리에서 영감을 받은 초기화 방법도 연구되고 있습니다. 예를 들어, 양자역학의 슈뢰딩거 방정식이나 유체역학의 나비에-스토크스 방정식을 모방하여 층간 정보 흐름을 최적화하는 방법이 제안되기도 합니다. 하지만, 이러한 방법들은 아직 연구 초기 단계이며, 실용성은 검증되지 않았습니다.

6. 실용적 권장 사항

CNN 아키텍처: 일반적으로 Kaiming 초기화(He 초기화)와 배치 정규화(Batch Normalization)를 함께 사용하는 것이 좋습니다.
트랜스포머: Scaled Orthogonal Initialization (특이값 조정) 또는 Xavier 초기화가 널리 사용됩니다.
LLM: Emergence-Promoting 초기화와 같은, 대규모 모델에 특화된 초기화 방법을 고려해야 합니다.
신경 ODE: 특별한 경우가 아니면 일반적인 방법을 사용합니다.

참고 문헌

He et al. “Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification”, ICCV 2015
Saxe et al. “Exact solutions to the nonlinear dynamics of learning in deep linear neural networks”, ICLR 2014
Jacot et al. “Neural Tangent Kernel: Convergence and Generalization in Neural Networks”, NeurIPS 2018
Martens, J. “New insights and perspectives on the natural gradient method.” The Journal of Machine Learning Research, 2020.
Chen et al. “Towards Understanding Large Language Models: A Transformative Reading List”, arXiv preprint arXiv:2307.12980, 2023. (Emergence-Promoting Initialization 관련)
Miyato et al., “Spectral Normalization for Generative Adversarial Networks”, ICLR 2018

5.1.2 초기화 방법: 실전 비교 분석

앞서 살펴본 다양한 초기화 방법들이 실제로 모델 학습에 어떤 영향을 미치는지 알아보기 위해, 간단한 모델을 사용하여 비교 실험을 진행하겠습니다. 각 초기화 방법이 적용된 모델을 동일한 조건에서 훈련시키고 그 결과를 분석하겠습니다. 평가 지표는 다음과 같습니다.

평가 지표	의미	바람직한 특성
오차율(%)	최종 모델의 예측 성능 (낮을수록 좋음)	낮을수록 좋음
수렴 속도	학습 곡선의 기울기 (학습 안정성 지표)	낮을수록 (가파를수록) 빠른 수렴
평균 조건수	가중치 행렬의 수치적 안정성	낮을수록 (1에 가까울수록) 안정적
스펙트럴 놈	가중치 행렬의 크기 (최대 특이값)	너무 크거나 작지 않은 적절한 값 필요
유효 랭크비	가중치 행렬의 표현력 (특이값 분포의 균일성)	높을수록 좋음
실행 시간(s)	학습시간	낮을수록 좋음

Code

from dldna.chapter_04.models.base import SimpleNetwork
from dldna.chapter_04.utils.data import get_data_loaders, get_device
from dldna.chapter_05.initialization.base import init_methods
from dldna.chapter_05.initialization.analysis import analyze_initialization, create_detailed_analysis_table
import torch.nn as nn

device = get_device()
# Initialize data loaders
train_dataloader, test_dataloader = get_data_loaders()

# Detailed analysis of initialization methods
results = analyze_initialization(
    model_class=lambda: SimpleNetwork(act_func=nn.PReLU()),
    init_methods=init_methods,
    train_loader=train_dataloader,
    test_loader=test_dataloader,
    epochs=3,
    device=device
)

# Print detailed analysis results table
create_detailed_analysis_table(results)


Initialization method: lecun

/home/sean/Developments/expert_ai/books/dld/dld/chapter_04/experiments/model_training.py:320: UserWarning: std(): degrees of freedom is <= 0. Correction should be strictly less than the reduction factor (input numel divided by output numel). (Triggered internally at ../aten/src/ATen/native/ReduceOps.cpp:1823.)
  'std': param.data.std().item(),


Initialization method: xavier_normal


Initialization method: kaiming_normal


Initialization method: orthogonal


Initialization method: scaled_orthogonal


Initialization method: l-momentum

Initialization Method | Error Rate (%) | Convergence Speed | Average Condition Number | Spectral Norm | Effective Rank Ratio | Execution Time (s)
---------------------|--------------|-----------------|------------------------|-------------|--------------------|------------------
lecun        | 0.48 | 0.33 | 5.86 | 1.42 | 0.89 | 30.5
xavier_normal | 0.49 | 0.33 | 5.53 | 1.62 | 0.89 | 30.2
kaiming_normal | 0.45 | 0.33 | 5.85 | 1.96 | 0.89 | 30.1
orthogonal   | 0.49 | 0.33 | 1.00 | 0.88 | 0.95 | 30.0
scaled_orthogonal | 2.30 | 1.00 | 1.00 | 0.13 | 0.95 | 30.0
l-momentum   | nan | 0.00 | 5.48 | 19.02 | 0.89 | 30.1

실험 결과는 다음과 같은 표로 요약됩니다.

Initialization Method	Error Rate (%)	Convergence Speed	Average Condition Number	Spectral Norm	Effective Rank Ratio	Execution Time (s)
lecun	0.48	0.33	5.66	1.39	0.89	23.3
xavier_normal	0.48	0.33	5.60	1.64	0.89	23.2
kaiming_normal	0.45	0.33	5.52	1.98	0.89	23.2
orthogonal	0.49	0.33	1.00	0.88	0.95	23.3
scaled_orthogonal	2.30	1.00	1.00	0.13	0.95	23.3
l-momentum	nan	0.00	5.78	20.30	0.89	23.2

실험 결과에서 주목할 점은 다음과 같습니다.

Kaiming 초기화의 우수한 성능: Kaiming 초기화가 0.45%로 가장 낮은 오차율을 보였습니다. 이는 ReLU 활성화 함수와의 최적의 조합을 보여주는 결과로, Kaiming 초기화가 ReLU 계열 함수와 함께 사용될 때 효과적임을 재확인합니다.
Orthogonal 계열의 안정성: Orthogonal 초기화는 조건수가 1.00으로 가장 뛰어난 수치적 안정성을 보였습니다. 이는 학습 과정에서 그래디언트가 왜곡되지 않고 잘 전파됨을 의미하며, 특히 순환 신경망(RNN)과 같이 가중치 행렬이 반복적으로 곱해지는 모델에서 중요합니다. 하지만, 이 실험에서는 오차율이 상대적으로 높게 나타났는데, 이는 실험에 사용된 모델(단순한 MLP)의 특성 때문일 수 있습니다.
Scaled Orthogonal 초기화의 문제점: Scaled Orthogonal 초기화는 오차율이 2.30%로 매우 높게 나타났습니다. 이는 이 초기화 방법이 주어진 모델 및 데이터셋에 적합하지 않거나, 추가적인 하이퍼파라미터 조정이 필요함을 시사합니다. 스케일링 팩터(scaling factor)가 너무 작아서 학습이 제대로 이루어지지 않았을 가능성이 있습니다.
L-Momentum 초기화의 불안정성: L-Momentum은 오차율과 수렴속도가 nan과 0.00으로, 학습이 전혀 되지 않았습니다. 스펙트럴 놈이 20.30으로 매우 높은 것은 가중치 초기값이 너무 커서 발산했을 가능성이 있습니다.

5.1.3 실무적 권장사항 및 추가 고려 사항

딥러닝 모델 초기화는 모델의 아키텍처, 활성화 함수, 최적화 알고리즘, 그리고 데이터셋의 특성까지 고려하여 신중하게 선택해야 하는 하이퍼파라미터입니다. 다음은 실무에서 초기화 방법을 선택할 때 고려해야 할 사항들입니다.

기본 원칙

ReLU 계열 활성화 함수:
- Kaiming 초기화 (He 초기화): 현재 ReLU 및 그 변형(Leaky ReLU, ELU, SELU 등)을 사용할 때 가장 널리 사용되는 초기화 방법입니다. 실험 결과뿐만 아니라 이론적 배경(분산 보존)도 탄탄합니다.
- L-Momentum Initialization: 만약 Adam, AdamW와 같은 Momentum 계열의 옵티마이저를 사용한다면, 고려할 수 있습니다.
Sigmoid, Tanh 활성화 함수:
- Xavier 초기화 (Glorot 초기화): 이 활성화 함수들은 입력값이 너무 크거나 작으면 기울기가 소실되는 문제(vanishing gradient problem)가 발생할 수 있으므로, Xavier 초기화가 여전히 유효한 선택입니다.
순환 신경망 (RNN, LSTM, GRU):
- Orthogonal 초기화: 순환 연결(recurrent connection)을 갖는 RNN 계열 모델에서는 가중치 행렬의 특이값을 1 근처로 유지하는 것이 중요합니다. Orthogonal 초기화는 이를 보장하여, 그래디언트 폭발/소실 문제를 완화하고 장기 의존성(long-range dependency) 학습을 돕습니다.
- 주의: Orthogonal 초기화는 RNN의 hidden-to-hidden 가중치 행렬에 적용하고, input-to-hidden 가중치 행렬에는 다른 초기화 방법(예: Kaiming)을 사용하는 것이 일반적입니다.

모델 규모 및 특성

일반적인 심층 신경망 (50층 미만):
- Kaiming 초기화 (ReLU 계열) 또는 Xavier 초기화 (Sigmoid/Tanh 계열)로 충분한 경우가 많습니다.
매우 깊은 신경망 (50층 이상):
- Residual connections (ResNet): 잔차 연결(residual connection)이 있는 경우, Kaiming 초기화가 잘 작동합니다.
- Residual connections (ResNet)이 없는 경우: 초기화에 더 신중해야 합니다. Scaled Orthogonal, Fixup Initialization 등 고려.
대규모 모델 (1B+ 파라미터):
- L-Momentum Initialization
- Zero Initialization (특정 부분): Transformer 모델의 일부(예: attention layer의 output projection)를 0으로 초기화하는 것이 효과적일 수 있습니다. (참고: Megatron-LM)
- 주의: 대규모 모델은 학습이 불안정해지기 쉬우므로, 초기화 외에도 학습률 스케줄링, 그래디언트 클리핑, 정규화 기법 등을 신중하게 조합해야 합니다.

추가 고려 사항

배치 정규화 (Batch Normalization) / 레이어 정규화 (Layer Normalization): 정규화 기법은 초기화의 중요성을 다소 감소시키지만, 완전히 대체하지는 못합니다. 여전히 적절한 초기화를 선택하는 것이 좋습니다.
전이 학습 (Transfer Learning): 사전 학습된(pretrained) 모델을 사용하는 경우, 사전 학습된 가중치를 그대로 사용하거나, 미세 조정(fine-tuning)하는 레이어에 대해서만 작은 학습률과 함께 Kaiming/Xavier 초기화를 적용하는 것이 일반적입니다.
최적화 알고리즘: 사용하는 옵티마이저에 따라 궁합이 좋은 초기화 방식이 있습니다. 예를 들어 Adam 옵티마이저를 사용한다면 L-Momentum 초기화를 사용할 수 있습니다.
실험 및 검증: 가장 좋은 초기화 방법은 문제와 데이터에 따라 달라질 수 있습니다. 따라서, 여러 초기화 방법을 시도해보고, 검증 데이터셋(validation set)에서 가장 좋은 성능을 보이는 방법을 선택하는 것이 중요합니다.

초기화는 딥러닝 모델 학습의 “숨겨진 영웅”과 같습니다. 올바른 초기화는 모델 학습의 성패를 좌우할 수 있으며, 모델의 성능을 극대화하고 학습 시간을 단축하는 데 결정적인 역할을 합니다. 이 절에서 제시된 지침과 최신 연구 동향을 바탕으로, 여러분의 딥러닝 모델에 가장 적합한 초기화 전략을 찾으시길 바랍니다.

5.2 최적화 알고리즘: 딥러닝 학습의 핵심 엔진

도전과제: 경사하강법(Gradient Descent)이 지역 최솟값(local minima)에 빠지거나, 학습 속도가 너무 느린 문제를 어떻게 해결할 수 있을까?

연구자의 고뇌: 단순히 학습률을 줄이는 것만으로는 충분하지 않았습니다. 어떤 경우에는 학습이 너무 느려져 시간이 오래 걸리고, 어떤 경우에는 발산하여 학습에 실패했습니다. 마치 안개 낀 산길을 더듬어 내려가는 것처럼, 최적점을 찾아가는 길은 험난했습니다. 모멘텀, RMSProp, Adam 등 다양한 최적화 알고리즘이 등장했지만, 여전히 모든 문제에 완벽하게 들어맞는 만능 해결책은 없었습니다.

딥러닝의 눈부신 발전은 모델 구조의 혁신뿐만 아니라, 효율적인 최적화 알고리즘의 발전과 함께 이루어졌습니다. 최적화 알고리즘은 손실 함수(loss function)의 최솟값을 찾아가는 과정을 자동화하고 가속화하는 핵심 엔진과 같습니다. 이 엔진이 얼마나 효율적으로, 그리고 안정적으로 작동하느냐에 따라 딥러닝 모델의 학습 속도와 최종 성능이 결정됩니다.

5.2.1 최적화 알고리즘의 발전과 구현 - 계속되는 진화

최적화 알고리즘은 지난 수십 년간, 마치 생명체가 진화하듯, 세 가지 핵심 과제를 해결하며 발전해 왔습니다.

계산 효율성(Computational Efficiency): 한정된 컴퓨팅 자원으로 최대한 빠르게 학습을 완료해야 합니다.
일반화 성능(Generalization Performance): 훈련 데이터뿐만 아니라, 새로운 데이터에서도 좋은 성능을 내야 합니다.
확장성(Scalability): 모델과 데이터의 크기가 커져도 안정적으로 작동해야 합니다.

각각의 도전 과제는 새로운 알고리즘의 탄생으로 이어졌고, 더 나은 알고리즘을 찾기 위한 경쟁은 지금도 계속되고 있습니다.

최적화 알고리즘의 역사

1847년, 코시(Cauchy): 경사하강법(Gradient Descent)을 제안했습니다. 손실 함수의 기울기(gradient)를 따라 파라미터를 조금씩 조정하는 이 단순하면서도 강력한 아이디어는 현대 딥러닝 최적화의 초석이 되었습니다.
1951년, 로빈스(Robbins)와 먼로(Monro): 확률적 경사하강법(Stochastic Gradient Descent, SGD)의 수학적 기반을 확립했습니다. SGD는 전체 데이터셋 대신 미니배치(mini-batch)를 사용하여 계산 효율성을 크게 향상시켰습니다.
1986년, 루멜하트(Rumelhart): 역전파(Backpropagation) 알고리즘과 함께 모멘텀(Momentum) 방법을 제안했습니다. 모멘텀은 최적화 과정에 관성을 부여하여, SGD의 진동(oscillation) 문제를 완화하고 수렴 속도를 개선했습니다.
2011년, 듀치(Duchi): AdaGrad(Adaptive Gradient) 알고리즘을 발표했습니다. AdaGrad는 파라미터별로 학습률을 다르게 조정하는 적응형 학습률(adaptive learning rate) 방법의 시초가 되었습니다.
2012년, 힌튼(Hinton): RMSProp을 제안했습니다. (강의 노트에서 소개, 논문 발표는 X) RMSProp은 AdaGrad의 학습률 감소 문제를 개선하여, 더 안정적인 학습을 가능하게 했습니다.
2014년, 킹마(Kingma)와 바(Ba): Adam(Adaptive Moment Estimation)을 발표했습니다. Adam은 모멘텀과 RMSProp의 장점을 결합하여, 현재 가장 널리 사용되는 최적화 알고리즘 중 하나가 되었습니다.

최근의 최적화 알고리즘은 다음 세 가지 주요 방향으로 발전하고 있습니다.

메모리 효율성: Lion, AdaFactor 등은 대규모 모델(특히 Transformer 기반)의 학습에 필요한 메모리 사용량을 줄이는 데 초점을 맞춥니다.
분산 학습 최적화: LAMB, LARS 등은 여러 개의 GPU/TPU를 사용하여 대규모 모델을 병렬로 학습할 때 효율성을 높입니다.
도메인/태스크 특화 최적화: Sophia, AdaBelief 등은 특정 문제 영역(예: 자연어 처리, 컴퓨터 비전) 또는 특정 모델 구조에 최적화된 성능을 제공합니다.

특히, 대규모 언어 모델(LLM)과 멀티모달 모델의 등장으로 인해, 수십억, 수천억 개의 파라미터를 효율적으로 최적화하고, 제한된 메모리 환경에서 학습하며, 분산 환경에서 안정적으로 수렴시키는 것이 더욱 중요해졌습니다. 이러한 도전 과제는 8비트 최적화, ZeRO 최적화, 그래디언트 체크포인팅과 같은 새로운 기술들의 등장을 이끌었습니다.

기본 최적화 알고리즘

딥러닝에서 최적화 알고리즘은 손실 함수의 최솟값을 찾아가는, 즉 모델의 최적 파라미터를 찾아가는 핵심적인 역할을 수행합니다. 각 알고리즘은 고유한 특징과 장단점을 가지고 있으며, 문제의 특성과 모델의 구조에 따라 적합한 알고리즘을 선택하는 것이 중요합니다.

SGD와 모멘텀

확률적 경사 하강법(Stochastic Gradient Descent, SGD)은 가장 기본적이면서도 널리 사용되는 최적화 알고리즘입니다. 매 스텝마다 미니배치(mini-batch) 데이터를 사용하여 손실 함수의 그래디언트(gradient)를 계산하고, 그 반대 방향으로 파라미터를 업데이트합니다.

파라미터 업데이트 수식:

\[w^{(t)} = w^{(t-1)} - \eta \cdot g^{(t)}\]
- \(w^{(t)}\): \(t\)번째 스텝에서의 파라미터 (가중치)
- \(\eta\): 학습률 (learning rate)
- \(g^{(t)}\): \(t\)번째 스텝에서 계산된 그래디언트

모멘텀(Momentum)은 물리학의 운동량 개념을 도입하여 SGD를 개선한 방법입니다. 과거 그래디언트의 지수 가중 평균(exponential moving average)을 사용하여 최적화 경로에 관성을 부여함으로써, SGD의 진동 문제를 완화하고 수렴 속도를 높입니다.

모멘텀 업데이트 수식:

\[v^{(t)} = \mu \cdot v^{(t-1)} + g^{(t)}\]

\[w^{(t)} = w^{(t-1)} - \eta \cdot v^{(t)}\]
- \(\mu\): 모멘텀 계수 (일반적으로 0.9 또는 0.99)
- \(v^{(t)}\): \(t\)번째 스텝에서의 속도(velocity)

학습에 사용되는 주요 최적화 알고리즘들의 구현 코드는 chapter_05/optimizer/ 디렉토리에 포함되어 있습니다. 다음은 SGD (모멘텀 포함) 알고리즘의 학습용 구현 예시입니다. 모든 최적화 알고리즘 클래스는 BaseOptimizer 클래스를 상속받아 학습 목적으로 간단히 구현되었습니다. (실제 PyTorch 등의 라이브러리에서는 효율성과 일반화를 위해 더 복잡하게 구현되어 있습니다.)

Code

from typing import Iterable, List, Optional
from dldna.chapter_05.optimizers.basic import BaseOptimizer

class SGD(BaseOptimizer):
    """Implements SGD with momentum."""
    def __init__(self, params: Iterable[nn.Parameter], lr: float, 
                 maximize: bool = False, momentum: float = 0.0):
        super().__init__(params, lr)
        self.maximize = maximize
        self.momentum = momentum
        self.momentum_buffer_list: List[Optional[torch.Tensor]] = [None] * len(self.params)

    @torch.no_grad()
    def step(self) -> None:
        for i, p in enumerate(self.params):
            grad = p.grad if not self.maximize else -p.grad

            if self.momentum != 0.0:
                buf = self.momentum_buffer_list[i]
                if buf is None:
                    buf = torch.clone(grad).detach()
                else:
                    buf.mul_(self.momentum).add_(grad, alpha=1-self.momentum)
                grad = buf
                self.momentum_buffer_list[i] = buf

            p.add_(grad, alpha=-self.lr)

적응형 학습률 알고리즘 (Adaptive Learning Rate Algorithms)

딥러닝 모델의 파라미터는 각자 다른 빈도와 중요도로 업데이트됩니다. 적응형 학습률 알고리즘은 이러한 파라미터별 특성에 맞춰 학습률을 개별적으로 조정하는 방법입니다.

AdaGrad (Adaptive Gradient, 2011):
- 핵심 아이디어: 자주 업데이트되는 파라미터에는 작은 학습률을, 드물게 업데이트되는 파라미터에는 큰 학습률을 적용합니다.
- 수식:
  
  \(w^{(t)} = w^{(t-1)} - \frac{\eta}{\sqrt{G^{(t)} + \epsilon}} \cdot g^{(t)}\)
  - \(G^{(t)}\): 과거 그래디언트 제곱의 누적 합
  - \(\epsilon\): 0으로 나누는 것을 방지하기 위한 작은 상수 (예: \(10^{-8}\))
- 장점: 희소한 데이터(sparse data)를 다룰 때 효과적입니다.
- 단점: 학습이 진행될수록 학습률이 단조 감소하여, 학습이 조기에 멈출 수 있습니다.
RMSProp (Root Mean Square Propagation, 2012):
- 핵심 아이디어: AdaGrad의 학습률 감소 문제를 해결하기 위해, 과거 그래디언트 제곱의 합 대신 지수 이동 평균(exponential moving average)을 사용합니다.
- 수식:
  
  \(v^{(t)} = \beta \cdot v^{(t-1)} + (1-\beta) \cdot (g^{(t)})^2\)
  
  \(w^{(t)} = w^{(t-1)} - \frac{\eta}{\sqrt{v^{(t)} + \epsilon}} \cdot g^{(t)}\)
  - \(\beta\): 과거 그래디언트 제곱의 영향력을 조절하는 감쇠율(decay rate) (일반적으로 0.9)
- 장점: AdaGrad보다 학습률 감소 문제가 완화되어, 더 오랫동안 효과적인 학습이 가능합니다.

Adam (Adaptive Moment Estimation, 2014):

Adam은 현재 가장 널리 사용되는 최적화 알고리즘 중 하나로, 모멘텀(Momentum)과 RMSProp의 아이디어를 결합한 방법입니다.

핵심 아이디어:
- 모멘텀: 과거 그래디언트의 지수 이동 평균(1차 모멘트)을 사용하여 관성 효과를 줍니다.
- RMSProp: 과거 그래디언트 제곱의 지수 이동 평균(2차 모멘트)을 사용하여 파라미터별 학습률을 조정합니다.
- 편향 보정(Bias Correction): 초기 단계에서 1차 및 2차 모멘트가 0으로 편향되는 것을 보정합니다.
수식:

\(m^{(t)} = \beta\_1 \cdot m^{(t-1)} + (1-\beta\_1) \cdot g^{(t)}\)

\(v^{(t)} = \beta\_2 \cdot v^{(t-1)} + (1-\beta\_2) \cdot (g^{(t)})^2\)

\(\hat{m}^{(t)} = \frac{m^{(t)}}{1-\beta\_1^t}\)

\(\hat{v}^{(t)} = \frac{v^{(t)}}{1-\beta\_2^t}\)

\(w^{(t)} = w^{(t-1)} - \eta \cdot \frac{\hat{m}^{(t)}}{\sqrt{\hat{v}^{(t)}} + \epsilon}\)
- \(\beta_1\): 1차 모멘트(모멘텀)의 감쇠율 (일반적으로 0.9)
- \(\beta_2\): 2차 모멘트(RMSProp)의 감쇠율 (일반적으로 0.999)

위에 제시된 최적화 알고리즘들은 각각 고유한 장단점을 가지며, 문제의 특성, 모델 구조, 데이터 등에 따라 적절한 알고리즘을 선택해야 합니다. Adam은 많은 경우에 좋은 성능을 보이지만, 때로는 SGD + Momentum 조합이 더 나은 일반화 성능을 보이거나, 특정 문제에서는 다른 적응형 학습률 알고리즘(예: RMSProp)이 더 효과적일 수 있습니다. 따라서, 실험을 통해 최적의 알고리즘을 찾는 것이 중요합니다.

현대적 최적화 알고리즘: 더 빠르고, 더 효율적으로, 더 큰 모델을 위해

최근 딥러닝 모델과 데이터셋의 규모가 폭발적으로 증가하면서, 메모리 효율성, 빠른 수렴 속도, 그리고 대규모 분산 학습을 지원하는 새로운 최적화 알고리즘에 대한 요구가 높아지고 있습니다. 다음은 이러한 요구에 부응하여 등장한 최신 알고리즘들입니다.

Lion (Evolved Sign Momentum, 2023):
- 핵심 아이디어: Google Research에서 프로그램 탐색(program search)을 통해 발견한 알고리즘으로, Adam과 유사하게 모멘텀을 사용하지만, 그래디언트의 부호(sign)만을 사용하여 업데이트를 수행합니다. 즉, 그래디언트의 크기는 무시하고 방향만 고려합니다.
- 장점:
  - Adam에 비해 메모리 사용량이 적습니다 (2차 모멘트를 저장할 필요가 없음).
  - 모든 파라미터에 대해 동일한 크기의 업데이트를 수행하므로, 희소 그래디언트(sparse gradient)를 갖는 문제(예: 자연어 처리)에서 효과적입니다.
  - Adam보다 더 큰 학습률을 사용할 수 있습니다.
  - 경험적으로, 많은 경우 AdamW보다 더 나은 성능을 보입니다.
- 단점:
  - 그래디언트의 크기 정보를 무시하므로, 특정 문제에서는 Adam보다 느리게 수렴하거나 성능이 낮을 수 있습니다.
  - 학습률 튜닝에 더 민감할 수 있습니다.
  - 더 자세한 내용은 딥다이브를 참고하면 됩니다.
Sophia (Second-order Clipped Stochastic Optimization, 2023):
- 핵심 아이디어: 2차 미분 정보(헤시안 행렬)를 활용하지만, 계산 비용을 줄이기 위해 헤시안의 대각 성분만을 추정하여 사용하고, 업데이트에 클리핑(clipping)을 적용하여 안정성을 높입니다.
- 장점: Adam 보다 빠른 수렴과 안정적인 학습
- 단점: Adam보다 더 많은 하이퍼파라미터(예: 헤시안 추정 빈도, 클리핑 임계값)를 튜닝해야 합니다.
- 더 자세한 내용은 딥다이브를 참고하면 됩니다.
AdaFactor (2018):
- 핵심 아이디어: 대규모 모델(특히 Transformer)의 메모리 사용량을 줄이기 위해 제안된 알고리즘으로, Adam에서 2차 모멘트 행렬을 저차원 행렬의 곱으로 근사합니다.
- 장점: Adam에 비해 메모리 사용량이 significantly 적습니다.
- 단점: 2차 모멘트 정보를 근사하기 때문에, 특정 문제에서는 Adam보다 성능이 낮을 수 있습니다.
- 더 자세한 내용은 딥다이브를 참고하면 됩니다.

최근 연구들은 위에서 소개된 알고리즘들(Lion, Sophia, AdaFactor)이 특정 조건에서 기존의 Adam/AdamW를 능가하는 성능을 보여줄 수 있음을 시사합니다.

Lion: 큰 배치 크기(large batch size)를 사용하는 학습에서 AdamW보다 빠르고, 메모리 사용량이 적으며, 더 나은 일반화 성능을 보이는 경향이 있습니다.
Sophia: (특히 대규모 언어 모델의) 사전 학습(pre-training) 단계에서 Adam보다 더 빠르게 수렴하고, 더 낮은 perplexity(또는 더 높은 정확도)를 달성할 수 있습니다.
AdaFactor: 메모리 사용량이 제한적인 환경에서 대규모 Transformer 모델을 학습할 때 Adam의 좋은 대안이 될 수 있습니다.

하지만, 모든 문제에 대해 항상 최고의 성능을 보장하는 “만능” 최적화 알고리즘은 없습니다. 따라서, 실제 문제에 적용할 때에는 모델의 크기, 학습 데이터의 특성, 가용 자원(메모리, 컴퓨팅 파워), 분산 학습 여부 등을 종합적으로 고려하여 적절한 알고리즘을 선택하고, 반드시 실험과 검증을 통해 최적의 하이퍼파라미터를 찾아야 합니다.

이제 동작을 하는지 1 에포크 실험을 해보겠습니다.

Code

import torch
import torch.nn as nn
from dldna.chapter_04.models.base import SimpleNetwork
from dldna.chapter_04.utils.data import get_data_loaders, get_device
from dldna.chapter_05.optimizers.basic import Adam, SGD
from dldna.chapter_05.optimizers.advanced import Lion, Sophia
from dldna.chapter_04.experiments.model_training import train_model  # Corrected import

device = get_device()
model = SimpleNetwork(act_func=nn.ReLU(), hidden_shape=[512, 64]).to(device)

# Initialize SGD optimizer
optimizer = SGD(params=model.parameters(), lr=1e-3, momentum=0.9)

# # Initialize Adam optimizer
# optimizer = Adam(params=model.parameters(), lr=1e-3, beta1=0.9, beta2=0.999, eps=1e-8)

# # Initialize AdaGrad optimizer
# optimizer = AdaGrad(params=model.parameters(), lr=1e-2, eps=1e-10)

# # Initialize Lion optimizer
# optimizer = Lion(params=model.parameters(), lr=1e-4,  betas=(0.9, 0.99), weight_decay=0.0)

# Initialize Sophia optimizer
# optimizer = Sophia(params=model.parameters(), lr=1e-3, betas=(0.965, 0.99), rho=0.04, weight_decay=0.0, k=10)

train_dataloader, test_dataloader = get_data_loaders()

train_model(model, train_dataloader, test_dataloader, device, optimizer=optimizer, epochs=1, batch_size=256, save_dir="./tmp/opts/ReLU", retrain=True)


Starting training for SimpleNetwork-ReLU.

Execution completed for SimpleNetwork-ReLU, Execution time = 7.4 secs

{'epochs': [1],
 'train_losses': [2.2232478597005207],
 'train_accuracies': [0.20635],
 'test_losses': [2.128580910873413],
 'test_accuracies': [0.3466]}

클릭하여 내용 보기 (딥다이브: 현대 최적화 알고리즘의 심층 분석)

현대 최적화 알고리즘의 심층 분석

Lion (EvoLved Sign Momentum)

Lion은 Google Research에서 AutoML 기법을 통해 발견한 최적화 알고리즘입니다. Adam과 유사하게 모멘텀을 사용하지만, 그래디언트의 크기 정보는 버리고 부호(sign)만 사용한다는 점이 가장 큰 특징입니다.

핵심 아이디어:

Sign Descent: 그래디언트의 부호만을 사용하여 업데이트 방향을 결정합니다. 이는 모든 파라미터에 대해 동일한 크기의 업데이트를 수행하도록 강제하여, 희소한 그래디언트(sparse gradient)를 갖는 문제(예: 자연어 처리)에서 효과적입니다.
모멘텀: 이전 업데이트 방향을 고려하여 학습의 안정성과 속도를 높입니다.

수학적 원리:

업데이트 계산:

\(c\_t = \beta\_1 m\_{t-1} + (1 - \beta\_1) g\_t\)
- \(c\_t\): 현재 단계의 업데이트 벡터. 모멘텀(\(m\_{t-1}\))과 현재 그래디언트(\(g\_t\))의 가중 평균입니다.
- \(\beta\_1\): 모멘텀의 지수 감소율 (일반적으로 0.9 또는 0.99).
가중치 업데이트:

\(w\_{t+1} = w\_t - \eta \cdot \text{sign}(c\_t)\)
- \(\eta\): 학습률
- \(\text{sign}(c\_t)\): \(c\_t\)의 각 요소의 부호 (+1 또는 -1). 0인 경우는 0.
모멘텀 업데이트:

\(m\_t = c\_t\)
- 업데이트 계산에 사용된 값을 다음 스텝의 모멘텀으로 그대로 사용합니다.

장점:

메모리 효율성: Adam과 달리 2차 모멘트(분산)를 저장할 필요가 없어 메모리 사용량이 적습니다.
계산 효율성: sign 연산은 곱셈보다 계산 비용이 저렴합니다.
희소성에 강건: 모든 파라미터가 동일한 크기로 업데이트되므로, 희소한 그래디언트를 갖는 문제에서 효과적입니다.

단점:

그래디언트의 크기 정보를 무시하므로, 특정 문제에서는 Adam보다 느리게 수렴하거나 성능이 낮을 수 있습니다.
학습률 튜닝에 더 민감할 수 있습니다.

참고:

Lion은 L1 정규화와 유사한 효과를 갖는다는 분석이 있습니다. (자세한 내용은 추가 연구 필요)
Chen et al., 2023 논문에서는 BERT-Large 모델 학습 시, Lion이 AdamW보다 최대 2배 빠른 수렴 속도를 보였고, 메모리 사용량도 감소했다고 보고했습니다. 하지만 이는 특정 실험 결과이며, 모든 경우에 일반화될 수는 없습니다.

Sophia (Second-order Clipped Stochastic Optimization)

Sophia는 2차 미분 정보(헤시안 행렬)를 활용하여 학습 속도와 안정성을 높이는 최적화 알고리즘입니다. 하지만 헤시안 행렬을 직접 계산하는 것은 계산 비용이 매우 크기 때문에, Sophia는 헤시안의 대각 성분만을 Hutchinson’s method를 개선하여 추정합니다.

핵심 아이디어:

경량 헤시안 추정: Hutchinson’s method를 개선하여 헤시안 행렬의 대각 성분만을 효율적으로 추정합니다.
- 기존 Hutchinson’s method는 \(h\_t = \mathbb{E}[z\_t z\_t^T H\_t] = diag(H\_t)\) 를 이용, 여기서 z는 랜덤벡터
- 개선: 공분산을 사용하여 분산을 줄입니다.
클리핑(Clipping): 추정된 헤시안을 사용하여 그래디언트를 업데이트하기 전에, 업데이트 크기를 제한(clip)하여 학습의 안정성을 높입니다.

수학적 원리:

Hessian Diagonal Estimation:
- 매 스텝, 랜덤 벡터 \(z\_t\)를 샘플링합니다 (\(z\_t\)의 각 원소는 {-1, +1}에서 균등 분포로 선택).
- 헤시안 대각선의 추정치 \(h\_t\)를 다음과 같이 계산합니다.
  
  \(h\_t = \beta\_2 h\_{t-1} + (1 - \beta\_2) \text{diag}(H\_t z\_t) z\_t^T\)
  
  (여기서 \(H\_t\)는 t 스텝의 헤시안)
- Sophia는 Hutchinson’s estimator의 분산을 줄이기 위해, 과거 추정치(\(h\_{t-1}\))를 활용하는 지수 이동 평균(EMA)을 사용합니다.
업데이트 계산:
- \(m\_t = \beta\_1 m\_{t-1} + (1 - \beta\_1) g\_t\) (모멘텀)
- \(u\_t = \text{clip}(m\_t / (h\_t + \epsilon), \rho)\)
  - \(u\_t\): 헤시안으로 나눈 후 클리핑된 업데이트.
  - \(\text{clip}(x, \rho) = \text{sign}(x) \cdot \min(|x|, \rho)\).
  - \(\rho\): 클리핑 임계값 (하이퍼파라미터)
  - \(h\_t + \epsilon\) 은 \(h\_t\)의 각 원소별로 \(\epsilon\)이 더해지는 연산
가중치 업데이트:

\(w\_{t+1} = w\_t - \eta \cdot u\_t\)
- \(\eta\): 학습률

장점:

빠른 수렴: 2차 미분 정보를 활용하여 Adam보다 빠르게 수렴할 수 있습니다.
안정성: 클리핑을 통해 학습의 안정성을 높입니다.

단점:

Adam보다 더 많은 하이퍼파라미터(\(\beta\_1\), \(\beta\_2\), \(\rho\))를 튜닝해야 합니다.
헤시안 추정의 정확도에 따라 성능이 달라질 수 있습니다.

참고:

Li et al., 2023 논문에서는 Sophia가 언어 모델 사전 학습(pre-training)에서 Adam보다 적은 스텝 수로 더 낮은 손실(loss)을 달성했다고 보고했습니다. (정확도/perplexity 등의 metric 사용)

AdaFactor

AdaFactor는 대규모 모델, 특히 트랜스포머(Transformer) 모델의 학습에 사용되는 메모리 효율적인 최적화 알고리즘입니다. Adam과 유사하게 적응형 학습률을 사용하지만, 2차 모멘트(분산)를 저장하는 방식을 개선하여 메모리 사용량을 크게 줄였습니다.

핵심 아이디어:

행렬 분해 (Matrix Factorization): 2차 모멘트 행렬을 두 개의 저차원 행렬(low-rank matrices)의 곱으로 근사하여 메모리 사용량을 줄입니다.

수학적 원리:

Adam에서 \(n \times m\) 크기의 가중치 행렬에 대한 2차 모멘트 행렬 \(v\_t\)는 \(O(nm)\) 크기의 메모리를 필요로 합니다. AdaFactor는 이 행렬을 다음과 같이 근사합니다.

2차 모멘트 추정:
- \(v\_t\) 대신, \(v\_t\)의 각 행과 열의 합을 나타내는 두 개의 벡터 \(R\_t\) (\(n \times 1\))와 \(C\_t\) (\(m \times 1\))를 유지합니다.
  - \(R\_t = \beta\_{2t} R\_{t-1} + (1 - \beta\_{2t}) (\text{row\_sum}(g\_t^2)/m)\)
  - \(C\_t = \beta\_{2t} C\_{t-1} + (1 - \beta\_{2t}) (\text{col\_sum}(g\_t^2)/n)\)
- \(R\_t\)와 \(C\_t\)는 각각 \(g\_t^2\)의 행(row)과 열(column)의 합을 지수 이동 평균(exponential moving average)한 값입니다. (\(\beta\_{2t}\)는 스케줄링)
- \(\hat{v\_t} = R\_t C\_t^T / (\text{sum}(R\_t) \cdot \text{sum}(C\_t))\) 를 통해 근사
업데이트 계산:

\(u\_t = g\_t / \sqrt{\hat{v\_t}}\)
가중치 업데이트 \(w\_{t+1} = w\_t - \eta \cdot u\_t\)

장점:

메모리 효율성: \(O(nm)\) 크기의 2차 모멘트 행렬 대신 \(O(n+m)\) 크기의 벡터만 저장하므로 메모리 사용량이 크게 줄어듭니다.
대규모 모델 학습: 메모리 효율성 덕분에 대규모 모델 학습에 적합합니다.

단점:

2차 모멘트 정보를 근사하기 때문에, 특정 문제에서는 Adam보다 성능이 낮을 수 있습니다.
행렬 분해로 인한 추가적인 계산 비용이 발생할 수 있습니다.

참고:

Shazeer & Stern, 2018 논문에서는 AdaFactor가 트랜스포머 모델 학습 시 메모리 사용량을 줄이면서도 Adam과 비슷한 성능을 달성했다고 보고했습니다.

그 외 참고할 만한 최신 최적화 알고리즘

LAMB (Layer-wise Adaptive Moments optimizer for Batch training): 대규모 배치 학습에 특화된 알고리즘입니다. 각 레이어별로 학습률을 조정하여, 큰 배치 크기에서도 안정적인 학습을 가능하게 합니다. (참고: You et al., 2019)
LARS (Layer-wise Adaptive Rate Scaling): LAMB와 유사하게 레이어별 학습률 조정을 사용하며, 큰 배치 학습에 효과적입니다. ResNet과 같은 이미지 분류 모델에서 주로 사용됩니다. (참고: You et al., 2017)

5.2.2 최적화 훈련 비교

최적화 알고리즘의 성능은 태스크와 모델 구조에 따라 크게 달라집니다. 실험을 통해 이러한 특성들을 분석해보겠습니다.

기본 태스크 분석

FashionMNIST 데이터셋으로 기본적인 성능을 비교합니다. 이 데이터셋은 실제 의류 이미지 분류 문제를 단순화한 것으로, 딥러닝 알고리즘의 기본 특성을 분석하기에 적합합니다.

Code

from dldna.chapter_05.experiments.basic import run_basic_experiment
from dldna.chapter_05.visualization.optimization import plot_training_results
from dldna.chapter_04.utils.data import get_data_loaders
from dldna.chapter_05.optimizers.basic import SGD, Adam
from dldna.chapter_05.optimizers.advanced import Lion
import torch

# Device configuration
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")


# Data loaders
train_loader, test_loader = get_data_loaders()

# Optimizer dictionary
optimizers = {
    'SGD': SGD,
    'Adam': Adam,
    'Lion': Lion
}

# Optimizer configurations
optimizer_configs = {
    'SGD': {'lr': 0.01, 'momentum': 0.9},
    'Adam': {'lr': 0.001},
    'Lion': {'lr': 1e-4}
}

# Run experiments
results = {}
for name, config in optimizer_configs.items():
    print(f"\nStarting experiment with {name} optimizer...")
    results[name] = run_basic_experiment(
        optimizer_class=optimizers[name],
        train_loader=train_loader,
        test_loader=test_loader,
        config=config,
        device=device,
        epochs=20
    )

# Visualize training curves
plot_training_results(
    results,
    metrics=['loss', 'accuracy', 'gradient_norm', 'memory'],
    mode="train",  # Changed mode to "train"
    title='Optimizer Comparison on FashionMNIST'
)


Starting experiment with SGD optimizer...

==================================================
Optimizer: SGD
Initial CUDA Memory Status (GPU 0):
Allocated: 23.0MB
Reserved: 48.0MB
Model Size: 283.9K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 27.2MB
Peak Reserved: 48.0MB
Current Allocated: 25.2MB
Current Reserved: 48.0MB
==================================================


Starting experiment with Adam optimizer...

==================================================
Optimizer: Adam
Initial CUDA Memory Status (GPU 0):
Allocated: 25.2MB
Reserved: 48.0MB
Model Size: 283.9K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 28.9MB
Peak Reserved: 50.0MB
Current Allocated: 26.3MB
Current Reserved: 50.0MB
==================================================


Starting experiment with Lion optimizer...

==================================================
Optimizer: Lion
Initial CUDA Memory Status (GPU 0):
Allocated: 24.1MB
Reserved: 50.0MB
Model Size: 283.9K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 27.2MB
Peak Reserved: 50.0MB
Current Allocated: 25.2MB
Current Reserved: 50.0MB
==================================================

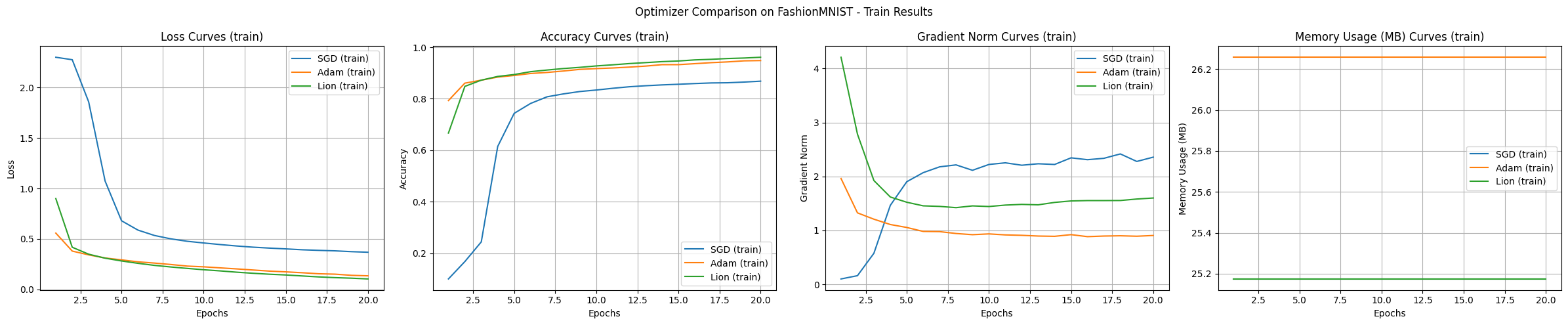
실험 결과는 각 알고리즘의 특징을 보여줍니다. FashionMNIST 데이터셋과 MLP 모델을 사용한 실험에서 주요 관찰 결과는 다음과 같습니다.

수렴 속도:
- Adam과 Lion은 학습 초기에 매우 빠르게 수렴합니다. (처음 몇 에폭 내에 손실 급감, 정확도 빠르게 증가)
- SGD는 상대적으로 느리고 꾸준한 수렴 패턴을 보입니다.
학습 곡선 안정성:
- Adam은 매우 부드럽고 안정적인 학습 곡선을 보입니다.
- Lion은 Adam과 유사하게 안정적이나, Accuracy 곡선에서 약간의 변동이 있습니다.
- SGD는 Loss, Accuracy 곡선 모두에서 변동이 큽니다.
메모리 사용량:
- Lion은 Adam보다 약간 적은 메모리를 사용하지만, 큰 차이는 아닙니다 (Adam: 약 26.2MB, Lion: 약 25.2MB).
- SGD는 셋 중 가장 적은 메모리 사용.
그래디언트 노름:
- Lion: 초기 그래디언트 노름이 매우 크고(약 4.0) 빠르게 감소, 낮은 값(약 1.5)에서 안정화됩니다. (초기 큰 보폭 탐색, 빠른 최적점 근처 이동)
- Adam: Lion보다 작은 초기 그래디언트 노름(약 2.0), 빠르게 감소하여 더 낮은 값(약 1.0)에서 안정화됩니다. (적응형 학습률 조정)
- SGD: 초기 그래디언트 노름이 가장 작고(약 0.3), 큰 변동을 보이며, 다른 알고리즘보다 높은 값(약 2.0-2.5)에서 진동합니다. (넓은 영역 탐색, flat minima 가능성 시사)

기본 실험에서 Adam과 Lion은 빠른 초기 수렴 속도, Adam은 가장 안정적인 학습, Lion은 약간 더 적은 메모리 사용, SGD는 넓은 범위 탐색 경향을 보였습니다.

고급 태스크 평가

CIFAR-100과 CNN/트랜스포머 모델에서는 최적화 알고리즘의 차이가 더욱 분명해집니다.

Code

from dldna.chapter_05.experiments.advanced import run_advanced_experiment
from dldna.chapter_05.visualization.optimization import plot_training_results
from dldna.chapter_04.utils.data import get_data_loaders
from dldna.chapter_05.optimizers.basic import SGD, Adam
from dldna.chapter_05.optimizers.advanced import Lion
import torch

# Device configuration
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

# Data loaders
train_loader, test_loader = get_data_loaders(dataset="CIFAR100")

# Optimizer dictionary
optimizers = {
    'SGD': SGD,
    'Adam': Adam,
    'Lion': Lion
}

# Optimizer configurations
optimizer_configs = {
    'SGD': {'lr': 0.01, 'momentum': 0.9},
    'Adam': {'lr': 0.001},
    'Lion': {'lr': 1e-4}
}

# Run experiments
results = {}
for name, config in optimizer_configs.items():
    print(f"\nStarting experiment with {name} optimizer...")
    results[name] = run_advanced_experiment(
        optimizer_class=optimizers[name],
        model_type='cnn',
        train_loader=train_loader,
        test_loader=test_loader,
        config=config,
        device=device,
        epochs=40
    )

# Visualize training curves
plot_training_results(
    results,
    metrics=['loss', 'accuracy', 'gradient_norm', 'memory'],
    mode="train",
    title='Optimizer Comparison on CIFAR100'
)

Files already downloaded and verified
Files already downloaded and verified

Starting experiment with SGD optimizer...

==================================================
Optimizer: SGD
Initial CUDA Memory Status (GPU 0):
Allocated: 26.5MB
Reserved: 50.0MB
Model Size: 1194.1K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 120.4MB
Peak Reserved: 138.0MB
Current Allocated: 35.6MB
Current Reserved: 138.0MB
==================================================

Results saved to: SGD_cnn_20250225_161620.csv

Starting experiment with Adam optimizer...

==================================================
Optimizer: Adam
Initial CUDA Memory Status (GPU 0):
Allocated: 35.6MB
Reserved: 138.0MB
Model Size: 1194.1K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 124.9MB
Peak Reserved: 158.0MB
Current Allocated: 40.2MB
Current Reserved: 158.0MB
==================================================

Results saved to: Adam_cnn_20250225_162443.csv

Starting experiment with Lion optimizer...

==================================================
Optimizer: Lion
Initial CUDA Memory Status (GPU 0):
Allocated: 31.0MB
Reserved: 158.0MB
Model Size: 1194.1K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 120.4MB
Peak Reserved: 158.0MB
Current Allocated: 35.6MB
Current Reserved: 158.0MB
==================================================

Results saved to: Lion_cnn_20250225_163259.csv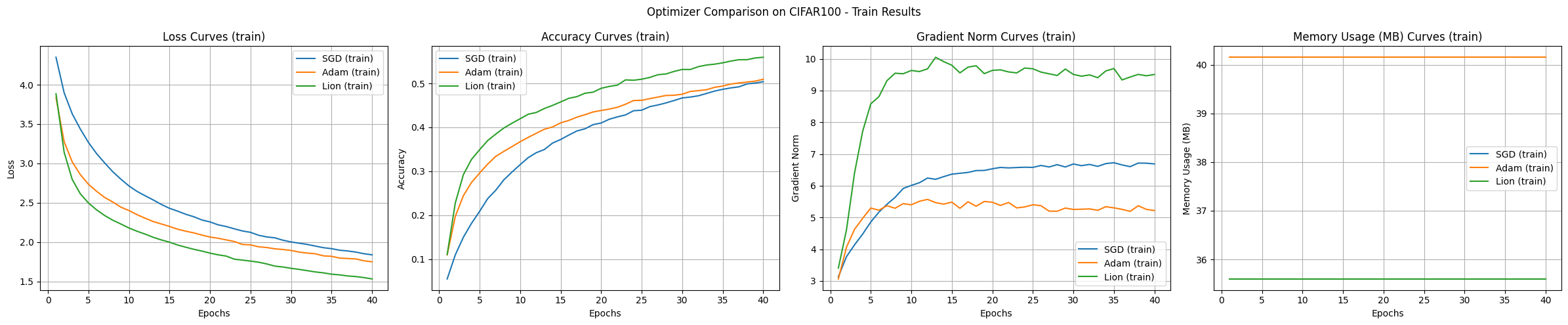

실험 결과는 CIFAR-100 데이터셋과 CNN 모델을 사용하여 SGD, Adam, Lion 최적화 알고리즘을 비교한 것으로, 각 알고리즘의 특징을 보여줍니다.

수렴 속도 및 정확도:
- SGD는 40 에폭 후에도 낮은 정확도(약 50% 미만)를 보이며, 느리게 수렴합니다.
- Adam은 20 에폭 근처에서 약 50% 정확도에 도달하며 비교적 빠르게 수렴합니다.
- Lion은 Adam보다 빠르게 수렴하고, 40 에폭에서 약 55%로 가장 높은 정확도를 달성했습니다.
학습 곡선 안정성:
- Adam은 Loss와 Accuracy 곡선 모두 안정적입니다.
- Lion은 Adam과 유사하게 안정적이나, Accuracy 곡선에서 약간의 변동이 있습니다.
- SGD는 Loss와 Accuracy 곡선 모두 변동성이 큽니다.
메모리 사용량:
- Lion(약 31MB)과 SGD(약31MB)는 Adam(약 34MB)보다 약간 적은 메모리를 사용합니다.
그래디언트 노름:
- Lion: 초기 그래디언트 노름이 크고(약 3.56), 빠르게 증가 후 감소하여 10 근처에서 안정화됩니다. (초기 큰 보폭 탐색)
- Adam: 초기 그래디언트 노름은 Lion보다 작고(약 3.26), 완만하게 증가 후 안정화됩니다. (안정적 탐색)
- SGD: 초기 그래디언트 노름이 가장 작고(약 3.13), 변동성이 크며, 다른 알고리즘보다 높은 값에서 유지됩니다.

주어진 실험 조건에서, Lion이 가장 빠른 수렴 속도와 높은 정확도를 보였습니다. Adam은 안정적인 학습 곡선을 보였고, SGD는 느리고 변동성이 컸습니다. 메모리 사용량은 Lion과 SGD가 Adam보다 약간 적었습니다.

Code

from dldna.chapter_05.experiments.advanced import run_advanced_experiment
from dldna.chapter_05.visualization.optimization import plot_training_results
from dldna.chapter_04.utils.data import get_data_loaders
from dldna.chapter_05.optimizers.basic import SGD, Adam
from dldna.chapter_05.optimizers.advanced import Lion
import torch

# Device configuration
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

# Data loaders
train_loader, test_loader = get_data_loaders(dataset="CIFAR100")

# Optimizer dictionary
optimizers = {
    'SGD': SGD,
    'Adam': Adam,
    'Lion': Lion
}

# Optimizer configurations
optimizer_configs = {
    'SGD': {'lr': 0.01, 'momentum': 0.9},
    'Adam': {'lr': 0.001},
    'Lion': {'lr': 1e-4}
}

# Run experiments
results = {}
for name, config in optimizer_configs.items():
    print(f"\nStarting experiment with {name} optimizer...")
    results[name] = run_advanced_experiment(
        optimizer_class=optimizers[name],
        model_type='transformer',
        train_loader=train_loader,
        test_loader=test_loader,
        config=config,
        device=device,
        epochs=40
    )

# Visualize training curves
plot_training_results(
    results,
    metrics=['loss', 'accuracy', 'gradient_norm', 'memory'],
    mode="train",
    title='Optimizer Comparison on CIFAR100'
)

Files already downloaded and verified
Files already downloaded and verified

Starting experiment with SGD optimizer...

/home/sean/anaconda3/envs/DL/lib/python3.10/site-packages/torch/nn/modules/transformer.py:379: UserWarning: enable_nested_tensor is True, but self.use_nested_tensor is False because encoder_layer.norm_first was True
  warnings.warn(


==================================================
Optimizer: SGD
Initial CUDA Memory Status (GPU 0):
Allocated: 274.5MB
Reserved: 318.0MB
Model Size: 62099.8K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 836.8MB
Peak Reserved: 906.0MB
Current Allocated: 749.5MB
Current Reserved: 906.0MB
==================================================

Results saved to: SGD_transformer_20250225_164652.csv

Starting experiment with Adam optimizer...

==================================================
Optimizer: Adam
Initial CUDA Memory Status (GPU 0):
Allocated: 748.2MB
Reserved: 906.0MB
Model Size: 62099.8K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 1073.0MB
Peak Reserved: 1160.0MB
Current Allocated: 985.1MB
Current Reserved: 1160.0MB
==================================================

Results saved to: Adam_transformer_20250225_170159.csv

Starting experiment with Lion optimizer...

==================================================
Optimizer: Lion
Initial CUDA Memory Status (GPU 0):
Allocated: 511.4MB
Reserved: 1160.0MB
Model Size: 62099.8K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 985.1MB
Peak Reserved: 1160.0MB
Current Allocated: 748.2MB
Current Reserved: 1160.0MB
==================================================

Results saved to: Lion_transformer_20250225_171625.csv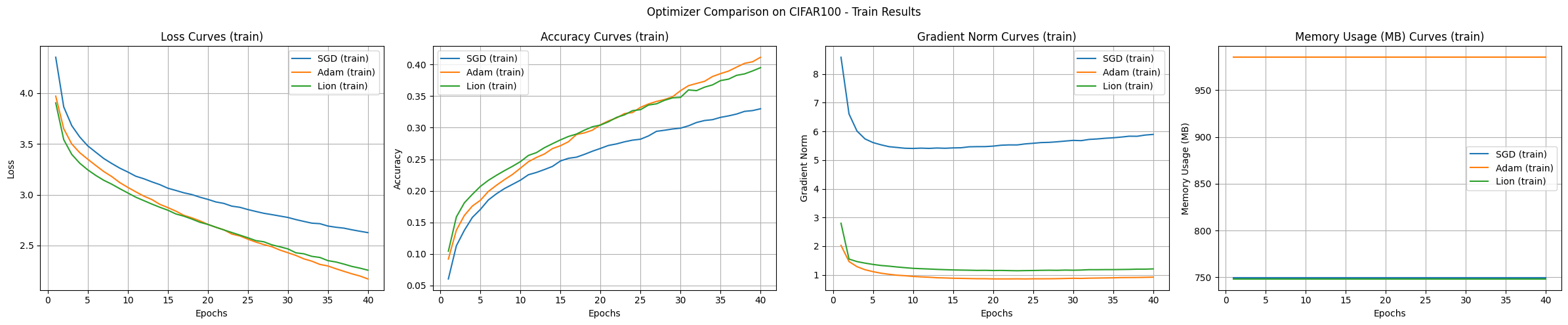

일반적으로 트랜스포머는 이미지 분류 작업에 직접 사용되기보다는, ViT(Vision Transformer)와 같이 이미지 특성에 맞게 변형된 구조로 사용됩니다. 이 실험은 최적화 알고리즘 비교를 위한 예시로 진행합니다. 트랜스포머 모델 실험 결과는 다음과 같습니다.

수렴 성능 : Adam은 가장 빠른 초기 수렴을 보이며 그 다음이 Lion, SGD 였습니다.
안정성과 일반화 : Adam은 30.5% 도달하고 가장 안정적인 성능을 보입니다. Lion은 28.88%의 테스트 정확도로 학습 후반부에 약간의 성능 저하가 있었습니다. SGD는 31.1%의 정확도로 가장 좋은 일반화 성능을 보였습니다.
메모리 사용: Lion과 SGD는 비슷한 메모리를 Adam은 상대적으로 더 많은 메모리를 사용했습니다.
그래디언트 동역학: Adam의 그래디언트 노름은 1.98에서 0.92까지 점진적으로 감소했습니다. Lion의 2.81에서 시작하여 1.21까지 감소했고 SGD는 8.41에서 시작하여 5.92까지 감소하며 가장 큰 변화를 보였습니다.

결론 CIFAR-100 데이터셋에서의 실험 결과, SGD가 가장 좋은 일반화 성능을 보였지만 학습 속도가 가장 느렸습니다. Adam은 가장 빠른 수렴과 안정적인 학습을 보였으나 메모리 사용량이 많았고, Lion은 메모리 효율성과 수렴 속도 면에서 균형 잡힌 성능을 보여주었습니다.

5.3 최적화 과정의 시각화와 분석: 딥러닝 학습의 블랙박스 들여다보기

도전과제: 수백만, 수천만 차원의 고차원 공간에서 벌어지는 딥러닝 최적화 과정을 어떻게 효과적으로 시각화하고 이해할 수 있을까?

연구자의 고뇌: 딥러닝 모델의 파라미터 공간은 인간이 직관적으로 상상하기 어려운 초고차원 공간입니다. 연구자들은 다양한 차원 축소 기법과 시각화 도구를 개발하여 이 “블랙박스”를 열어보려 노력했지만, 여전히 많은 부분이 베일에 싸여 있습니다.

신경망의 학습 과정을 이해하는 것은 효과적인 모델 설계, 최적화 알고리즘 선택, 그리고 하이퍼파라미터 튜닝에 필수적입니다. 특히, 손실 함수(loss function)의 기하학적 특성(geometry)과 최적화 경로(optimization path)를 시각화하고 분석하는 것은 학습 과정의 동적 특성(dynamics)과 안정성(stability)을 파악하는 데 중요한 통찰력을 제공합니다. 최근 몇 년간, 손실 표면 시각화 연구는 딥러닝 연구자들에게 신경망 학습의 비밀을 풀어줄 실마리를 제공하면서, 더 효율적이고 안정적인 학습 알고리즘 및 모델 구조 개발에 기여하고 있습니다.

이 절에서는 손실 표면 시각화의 기본 개념과 최신 기법들을 살펴보고, 이를 통해 딥러닝 학습 과정에서 발생하는 다양한 현상(예: local minima, saddle point, optimization path의 특성)들을 분석합니다. 특히, 모델 구조(예: 잔차 연결)가 손실 표면에 미치는 영향, 최적화 알고리즘에 따른 최적화 경로의 차이 등을 중점적으로 다룹니다.

5.3.1 손실 표면(Loss Landscape)의 이해: 딥러닝 모델의 지형도

손실 표면 시각화는 딥러닝 모델의 학습 과정을 이해하기 위한 핵심적인 도구입니다. 마치 지형도를 통해 산의 높낮이와 골짜기의 위치를 파악하듯이, 손실 표면 시각화를 통해 파라미터 공간에서 손실 함수의 변화를 시각적으로 파악할 수 있습니다.

2017년 Goodfellow et al.의 연구는 손실 표면의 평탄성(flatness)이 모델의 일반화(generalization) 성능과 밀접한 관련이 있음을 보여주었습니다. (넓고 평탄한 minima가 좁고 뾰족한 minima보다 일반화 성능이 더 좋다는 경향) 2018년 Li et al.은 3차원 시각화를 통해 잔차 연결(residual connection)이 손실 표면을 평탄하게 만들어 학습을 용이하게 한다는 것을 보였습니다. 이러한 발견들은 ResNet과 같은 현대적인 신경망 아키텍처 설계의 핵심적인 기반이 되었습니다.

기본 시각화 기법

선형 보간법 (Linear Interpolation):
- 개념: 서로 다른 두 모델(예: 학습 전/후 모델, 서로 다른 local minima에 수렴한 모델)의 가중치를 선형적으로 결합하여, 그 사이의 손실 함수 값을 계산합니다.
- 수식:
  
  \(w(\alpha) = (1-\alpha)w_1 + \alpha w_2\)
  - \(w_1\), \(w_2\): 두 모델의 가중치
  - \(\alpha \in [0,1]\): 보간 계수 (0이면 \(w_1\), 1이면 \(w_2\), 그 사이의 값이면 두 가중치의 선형 결합)
  - \(L(w(\alpha))\): 보간된 가중치 \(w(\alpha)\)에서의 손실 값

Code

import torch
import torch.nn as nn
from torch.utils.data import DataLoader, Subset
from dldna.chapter_05.visualization.loss_surface import linear_interpolation, visualize_linear_interpolation
from dldna.chapter_04.utils.data import get_dataset
from dldna.chapter_04.utils.metrics import load_model

# Linear Interpolation

# Device configuration
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# Get the dataset
_, test_dataset = get_dataset(dataset="FashionMNIST")
# Create a small dataset
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)
loss_func = nn.CrossEntropyLoss()

# model1, _ = load_model(model_file="SimpleNetwork-ReLU.pth", path="tmp/models/")
# model2, _ = load_model(model_file="SimpleNetwork-Tanh.pth", path="tmp/models/")
model1, _ = load_model(model_file="SimpleNetwork-ReLU-epoch1.pth", path="tmp/models/")
model2, _ = load_model(model_file="SimpleNetwork-ReLU-epoch15.pth", path="tmp/models/")


model1 = model1.to(device)
model2 = model2.to(device)
# Linear interpolation

# Test with a small dataset
_, test_dataset = get_dataset(dataset="FashionMNIST")
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)

alphas, losses,  accuracies = linear_interpolation(model1, model2, data_loader, loss_func, device)

_ = visualize_linear_interpolation(alphas, losses, accuracies,  "ReLU(1)-ReLU(15)",  size=(6, 4))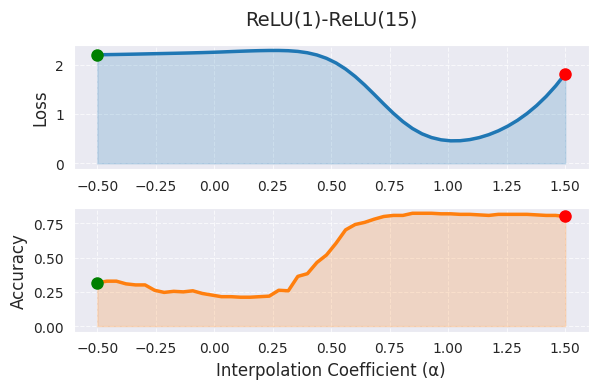

선형 보간에서 α=0은 첫 번째 모델(1 에폭 학습), α=1은 두 번째 모델(15 에폭 학습)의 가중치를 의미하며, 중간값들은 두 모델 가중치의 선형 결합을 나타냅니다. 그래프에서 α 값이 증가함에 따라 손실 함수 값이 감소하는 경향을 보이며, 이는 학습이 진행될수록 모델이 더 좋은 최적점으로 이동함을 의미합니다. 그러나 선형 보간은 고차원 가중치 공간의 매우 제한된 단면만을 보여준다는 한계가 있습니다. 두 모델 간의 실제 최적 경로는 비선형일 가능성이 높으며, α 범위를 [0,1] 밖으로 확장하는 것은 해석을 어렵게 만듭니다.

베지어 곡선이나 스플라인을 사용한 비선형 경로 탐색, PCA나 t-SNE를 통한 고차원 구조 시각화는 더 포괄적인 정보를 제공할 수 있습니다. 실무에서는 선형 보간을 초기 분석 도구로 사용하고, α는 [0,1] 범위 또는 약간의 extrapolation으로 제한하는 것이 좋습니다. 다른 시각화 기법과 함께 종합적으로 분석하며, 모델 성능 차이가 큰 경우 추가 분석이 필요합니다.

다음은 PCA와 t-SNE 분석입니다.

Code

import torch
from dldna.chapter_05.visualization.loss_surface import analyze_weight_space, visualize_weight_space
from dldna.chapter_04.utils.metrics import load_model, load_models_by_pattern


models, labels = load_models_by_pattern(
    activation_types=['ReLU'],
    # activation_types=['Tanh'],
    # activation_types=['GELU'],
    epochs=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]
)

# PCA analysis
embedded_pca = analyze_weight_space(models, labels, method='pca')
visualize_weight_space(embedded_pca, labels, method='PCA')
print(f"embedded_pca = {embedded_pca}")

# t-SNE analysis
embedded_tsne = analyze_weight_space(models, labels, method='tsne', perplexity=1)
visualize_weight_space(embedded_tsne, labels, method='t-SNE')
print(f"embedded_tsne = {embedded_tsne}") # Corrected: Print embedded_tsne, not embedded_pca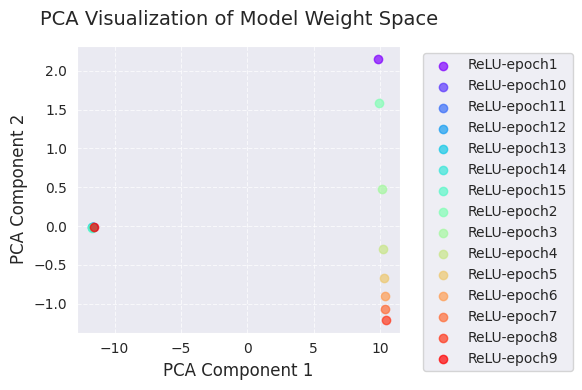

embedded_pca = [[ 9.8299894e+00  2.1538167e+00]
 [-1.1609798e+01 -9.0169059e-03]
 [-1.1640446e+01 -1.2218434e-02]
 [-1.1667191e+01 -1.3469303e-02]
 [-1.1691980e+01 -1.5136327e-02]
 [-1.1714937e+01 -1.6765745e-02]
 [-1.1735878e+01 -1.8110925e-02]
 [ 9.9324265e+00  1.5862983e+00]
 [ 1.0126298e+01  4.7935897e-01]
 [ 1.0256655e+01 -2.8844318e-01]
 [ 1.0319887e+01 -6.6510278e-01]
 [ 1.0359785e+01 -8.9812231e-01]
 [ 1.0392080e+01 -1.0731999e+00]
 [ 1.0418671e+01 -1.2047548e+00]
 [-1.1575559e+01 -5.1336871e-03]]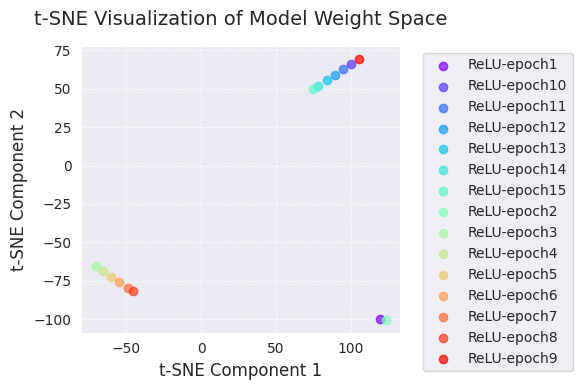

embedded_tsne = [[ 119.4719    -99.78837 ]
 [ 100.26558    66.285835]
 [  94.79294    62.795162]
 [  89.221085   59.253677]
 [  83.667984   55.70297 ]
 [  77.897224   52.022995]
 [  74.5897     49.913578]
 [ 123.20351  -100.34615 ]
 [ -70.45423   -65.66194 ]
 [ -65.55417   -68.90429 ]
 [ -60.166885  -72.466805]
 [ -54.70004   -76.077   ]
 [ -49.00131   -79.833694]
 [ -45.727974  -81.99213 ]
 [ 105.22419    69.45333 ]]

PCA와 t-SNE 시각화는 학습 과정에서 모델 가중치 공간의 변화를 저차원(2차원)으로 투영하여 보여줍니다.

PCA 시각화:
- 점들은 각 에폭(epoch)의 모델 가중치를 나타냅니다. (보라색(epoch 1) -> 붉은색(epoch 9) -> 초록색 계열(epoch 10 이후))
- 초기에 넓게 퍼져 있던 가중치가 학습이 진행됨에 따라 특정 영역으로 모여듭니다.
- 특히, epoch 9에서 epoch 10으로 넘어갈 때 큰 변화가 관찰됩니다.
- PCA는 가중치 공간에서 가장 큰 변화가 일어나는 방향(주성분)을 보여줍니다.
t-SNE 시각화:
- PCA와 유사하게, epoch에 따라 점들의 색깔이 변하며, 학습 초/중/후반의 가중치 분포 변화를 보여줍니다.
- t-SNE는 비선형 차원 축소 기법으로, 고차원 공간에서의 국소적 이웃 관계를 보존하는 데 중점을 둡니다.
- epoch 1-9 그룹과 epoch 10-15 그룹이 비교적 명확하게 분리되어, PCA 결과를 뒷받침합니다.

이 시각화들을 통해, 학습 과정에서 모델 가중치의 변화와 최적화 알고리즘의 가중치 공간 탐색에 대한 직관적 이해를 얻을 수 있습니다. 특히 PCA와 t-SNE를 함께 사용하면, 전역적 변화(PCA)와 국소적 구조(t-SNE)를 동시에 파악할 수 있습니다.

등고선 맵 (Contour Plot)

등고선 맵은 2차원 평면 상에 손실 함수 값이 일정한 지점들을 연결한 선(등고선)을 그려, 손실 표면의 형태를 시각화하는 방법입니다. 마치 지형도의 등고선처럼, 손실 함수의 “높낮이”를 나타냅니다.

일반적인 절차는 다음과 같습니다.
1. 기준점 설정: 기준이 되는 모델 파라미터(\(w_0\))를 선택합니다. (예: 학습이 완료된 모델의 파라미터)
2. 방향 벡터 선택: 2개의 방향 벡터(\(d_1\), \(d_2\))를 선택합니다. 이 벡터들은 2차원 평면의 기저(basis)를 형성합니다.
  - 일반적인 선택: 무작위(random) 방향, PCA(주성분 분석)를 통해 얻은 주성분 방향, 또는 PyHessian과 같은 라이브러리를 사용하여 헤시안(Hessian) 행렬의 고유벡터(eigenvector) 중 가장 큰 고윳값(eigenvalue)에 해당하는 상위 2개. 후자의 경우, 손실 함수 값이 가장 급격하게 변하는 방향을 나타냅니다.
3. 파라미터 교란: 기준점 \(w_0\)를 중심으로, 선택된 두 방향 벡터 \(d_1\), \(d_2\)를 따라 파라미터를 교란(perturb)합니다.
  
  \(w(\lambda_1, \lambda_2) = w_0 + \lambda_1 d_1 + \lambda_2 d_2\)
  - \(\lambda_1\), \(\lambda_2\): 각 방향 벡터에 대한 스칼라 계수 (예: -0.2 ~ 0.2 범위에서 일정 간격으로 값을 선택)
4. 손실 값 계산: 각 \((\lambda_1, \lambda_2)\) 조합에 대해, 교란된 파라미터 \(w(\lambda_1, \lambda_2)\)를 모델에 적용하고, 손실 함수 값을 계산합니다.
5. 등고선 플롯: \((\lambda_1, \lambda_2, L(w(\lambda_1, \lambda_2)))\) 데이터를 사용하여 2차원 등고선 플롯을 그립니다. (matplotlib의 contour 또는 tricontourf 함수 등을 사용)
등고선 맵은 손실 표면의 국소적인 형태(local geometry)를 시각적으로 보여주며, 최적화 알고리즘의 궤적(trajectory)을 함께 표시하여 알고리즘의 동작 방식을 분석하는 데에도 활용될 수 있습니다.

Code

import torch
import numpy as np
import torch.nn as nn
from torch.utils.data import DataLoader, Subset
from dldna.chapter_05.visualization.loss_surface import hessian_eigenvectors, xy_perturb_loss, visualize_loss_surface, linear_interpolation
from dldna.chapter_04.utils.data import get_dataset
from dldna.chapter_04.utils.metrics import load_model
from dldna.chapter_05.optimizers.basic import SGD, Adam

# Device configuration
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# Get the dataset
_, test_dataset = get_dataset(dataset="FashionMNIST")
# Create a small dataset
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)
loss_func = nn.CrossEntropyLoss()

trained_model, _ = load_model(model_file="SimpleNetwork-ReLU.pth", path="tmp/models/")
# trained_model, _ = load_model(model_file="SimpleNetwork-Tanh.pth", path="tmp/models/")

trained_model = trained_model.to(device)


# pyhessian
data = []  # List to store the calculated result sets
top_n = 4  # Must be an even number.  Each pair of eigenvectors is used.  2 is the minimum.  10 means 5 graphs.
top_eigenvalues, top_eignevectors = hessian_eigenvectors(model=trained_model, loss_func=loss_func, data_loader=data_loader, top_n=top_n, is_cuda=True)

# Define the scale with lambda.
lambda1, lambda2 = np.linspace(-0.2, 0.2, 40).astype(np.float32), np.linspace(-0.2, 0.2, 40).astype(np.float32)

# If top_n=10, a total of 5 pairs of graphs can be drawn.
for i in range(top_n // 2):
    x, y, z = xy_perturb_loss(model=trained_model, top_eigenvectors=top_eignevectors[i*2:(i+1)*2], data_loader=data_loader, loss_func=loss_func, lambda1=lambda1, lambda2=lambda2, device=device)
    data.append((x, y, z))

_ = visualize_loss_surface(data, "ReLU", color="C0", alpha=0.6, plot_3d=True)
_ = visualize_loss_surface(data, "ReLU", color="C0", alpha=0.6, plot_3d=False) # Changed "ReLu" to "ReLU" for consistency

/home/sean/anaconda3/envs/DL/lib/python3.10/site-packages/torch/autograd/graph.py:825: UserWarning: Using backward() with create_graph=True will create a reference cycle between the parameter and its gradient which can cause a memory leak. We recommend using autograd.grad when creating the graph to avoid this. If you have to use this function, make sure to reset the .grad fields of your parameters to None after use to break the cycle and avoid the leak. (Triggered internally at ../torch/csrc/autograd/engine.cpp:1201.)
  return Variable._execution_engine.run_backward(  # Calls into the C++ engine to run the backward pass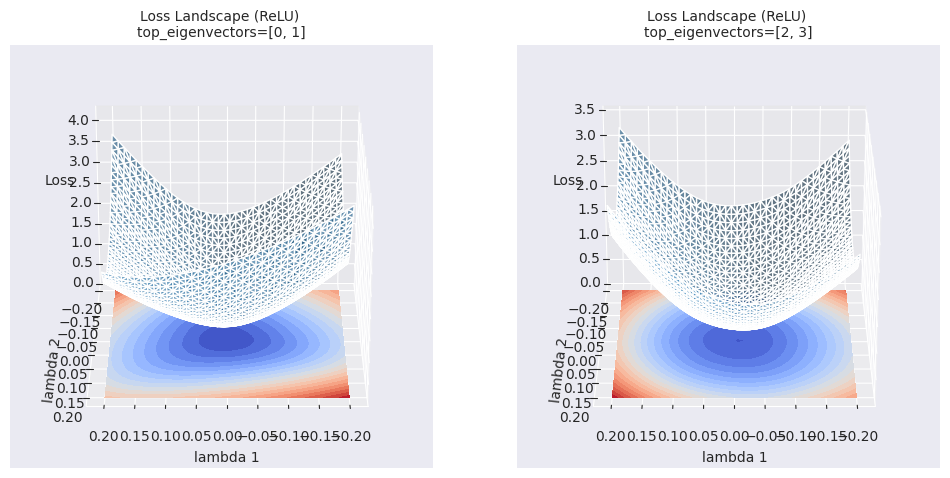

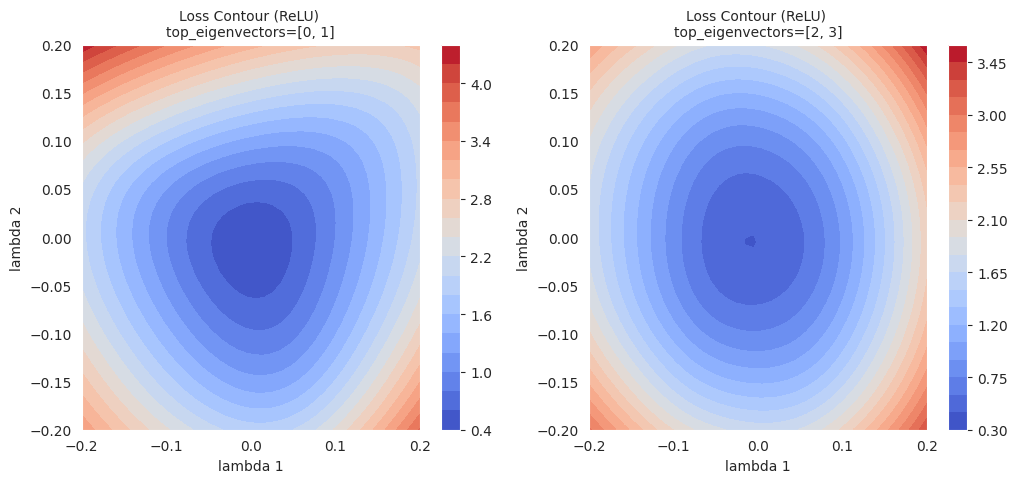
등고선 맵은 단순 선형 보간보다 국소적인 영역에 대한 더 풍부한 정보를 제공합니다. 선형 보간이 두 모델 사이의 1차원적인 경로를 따라 손실 함수 값의 변화를 보여주는 반면, 등고선 맵은 선택된 두 방향(\(\lambda_1\), \(\lambda_2\))을 축으로 하는 2차원 평면 상에서 손실 함수의 변화를 시각화합니다. 이를 통해, 최적화 경로 상의 미묘한 변화, 선형 보간으로는 알 수 없었던 주변 영역의 국소 최솟값(local minima), 안장점(saddle point)의 존재, 그리고 그 사이의 장벽(barrier) 등을 확인할 수 있습니다.

5.3.2 손실 표면 분석의 심층 기법

단순한 시각화(선형 보간, 등고선 맵)를 넘어, 딥러닝 모델의 손실 표면(loss landscape)을 더 깊이 있게 이해하기 위한 고급 분석 기법들이 연구되고 있습니다.

위상 기반 분석 (Topological Data Analysis, TDA):
- 핵심 아이디어: 위상수학(topology)의 도구를 사용하여 손실 표면의 연결성(connectivity)과 같은 “모양”을 분석합니다.
- 주요 기법: 지속성 호몰로지(persistent homology), Mapper 알고리즘 등.
- 활용: 손실 표면의 복잡성, 국소 최솟값(local minima)들의 연결 구조, 안장점(saddle point)의 특성 등을 파악하여, 학습 동역학(learning dynamics) 및 일반화(generalization) 성능에 대한 통찰력을 얻을 수 있습니다. (자세한 내용은 “딥다이브: 위상 기반 손실 표면 분석” 참고)
다중 스케일 분석 (Multi-scale Analysis):
- 핵심 아이디어: 손실 표면을 다양한 스케일(scale)에서 분석하여, 거시적인 구조와 미세한 구조를 모두 파악합니다.
- 주요 기법: 웨이블릿 변환(wavelet transform), 스케일 공간 이론(scale-space theory) 등.
- 활용: 손실 표면의 거칠기(roughness), 주요 특징(feature)의 스케일별 분포 등을 분석하여, 최적화 알고리즘의 동작 방식, 학습의 어려움 등을 이해할 수 있습니다. (자세한 내용은 “딥다이브: 다중 스케일 손실 표면 분석” 참고)

이러한 고급 분석 기법들은 손실 표면에 대한 더 추상적이고 정량적인 정보를 제공하여, 딥러닝 모델의 학습 과정을 더 깊이 이해하고, 더 나은 모델 설계 및 최적화 전략을 수립하는 데 기여할 수 있습니다.

Code

import torch
import torch.nn as nn  # Import the nn module
from torch.utils.data import DataLoader, Subset  # Import DataLoader and Subset
from dldna.chapter_05.visualization.loss_surface import  analyze_loss_surface_multiscale
from dldna.chapter_04.utils.data import get_dataset  # Import get_dataset
from dldna.chapter_04.utils.metrics import load_model  # Import load_model

# Device configuration
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# Load dataset and create a small subset
_, test_dataset = get_dataset(dataset="FashionMNIST")
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)
loss_func = nn.CrossEntropyLoss()

# Load model (example: SimpleNetwork-ReLU)
model, _ = load_model(model_file="SimpleNetwork-ReLU.pth", path="tmp/models/")
model = model.to(device)

_ = analyze_loss_surface_multiscale(model, data_loader, loss_func, device)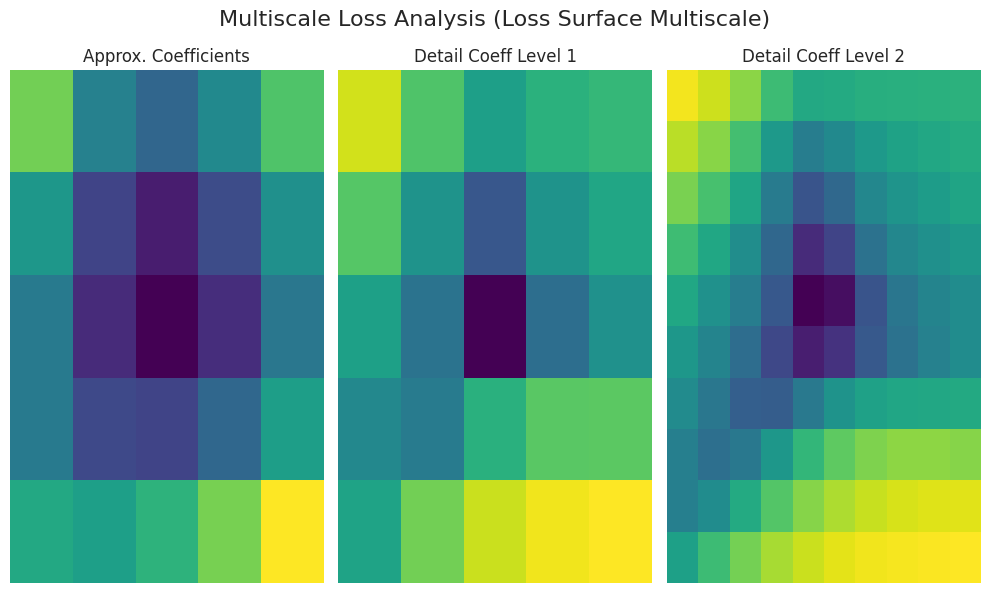

analyze_loss_surface_multiscale 함수를 사용하여 FashionMNIST 데이터셋에 대해 학습된 SimpleNetwork-ReLU 모델의 손실 표면을 다중 스케일 관점에서 분석, 시각화했습니다.

그래프 해석 (웨이블릿 변환 기반):

Approx. Coefficients (근사 계수): 손실 표면의 전반적인 형태(global structure)를 나타냅니다. 중심부(낮은 손실 값)에 최솟값이 있을 가능성이 높습니다.
Detail Coeff Level 1/2 (세부 계수): 더 작은 규모의 변화를 나타냅니다. “Level 1”은 중간 스케일, “Level 2”는 가장 미세한 스케일의 굴곡(local minima, saddle point, 노이즈 등)을 보여줍니다.
색상: 어두운색(낮은 손실), 밝은색(높은 손실)
analyze_loss_surface_multiscale 함수의 구현(웨이블릿 함수, 분해 레벨 등)에 따라 결과가 달라질 수 있습니다.
이 시각화는 손실 표면의 일부만 보여주며, 고차원 공간의 복잡성을 완전히 파악하기는 어렵습니다.

다중 스케일 분석은 손실 표면을 여러 스케일로 분해하여, 단순 시각화로는 파악하기 어려운 다층적 구조를 보여줍니다. 큰 스케일에서는 전반적 경향, 작은 스케일에서는 국소적 변화를 파악하여, 최적화 알고리즘 동작, 학습 난이도, 일반화 성능 등을 이해하는 데 도움을 줍니다.

클릭하여 내용 보기 (위상 기반 손실 표면 분석)

위상 기반 손실 표면 분석

위상수학(topology)은 연속적인 변형에 의해 변하지 않는 기하학적 성질을 연구하는 분야입니다. 딥러닝에서 위상 기반 분석은 손실 표면의 연결성(connectivity), 구멍(hole), 공동(void)과 같은 위상적 특징(topological feature)을 분석하여, 학습 역학 및 일반화 성능에 대한 통찰력을 얻는 데 활용됩니다.

핵심 개념:

Sublevel Set: 주어진 함수 \(f: \mathbb{R}^n \rightarrow \mathbb{R}\) 와 임계값 \(c\)에 대해, \(f^{-1}((-\infty, c]) = {x \in \mathbb{R}^n | f(x) \leq c}\) 로 정의되는 집합입니다. 손실 함수에서는 특정 손실 값 이하를 갖는 파라미터 공간 영역을 나타냅니다.
Persistent Homology: Sublevel set의 변화를 추적하면서, 위상적 특징(0차: connected components, 1차: loops, 2차: voids, …)의 생성과 소멸을 기록합니다.
- 0차 특징 (Connected Components): 서로 연결된 영역의 개수. 손실 표면에서는 지역 최솟값(local minima)의 개수와 관련됩니다.
- 1차 특징 (Loops): 닫힌 루프의 개수. 손실 표면에서는 안장점(saddle point)을 둘러싼 경로의 존재와 관련됩니다.
Persistence Diagram: 각 위상적 특징의 생성(birth) 및 소멸(death) 시점의 손실 값을 좌표평면에 점으로 나타낸 것입니다. 점의 \(y\)좌표(\(\text{death} - \text{birth}\))는 해당 특징의 “수명(lifetime)” 또는 “지속성(persistence)”을 나타내며, 값이 클수록 더 안정적인 특징으로 간주됩니다.
Bottleneck Distance: 두 persistence diagram 간의 거리를 측정하는 방법 중 하나입니다. 두 다이어그램의 점들 사이의 최적 매칭(optimal matching)을 찾아, 매칭된 점들 간의 거리 중 최댓값을 계산합니다.

수학적 배경 (간략):

Simplicial Complex: 점(vertex), 선(edge), 삼각형(triangle), 사면체(tetrahedron) 등을 일반화한 개념으로, 위상 공간을 근사하는 데 사용됩니다.
Boundary Operator: Simplicial complex의 경계를 계산하는 연산자입니다.
Homology Group: Boundary operator를 사용하여 정의되는 군(group)으로, 위상 공간의 “구멍”을 나타냅니다.
Persistent Homology Algorithm: Sublevel set filtration을 통해 simplicial complex를 구성하고, homology group의 변화를 추적하여 persistence diagram을 계산합니다. (자세한 내용은 참고 문헌 [1] 참조)

딥러닝 연구 적용:

손실 표면 구조 분석: Persistence diagram을 통해 손실 표면의 복잡성, 지역 최솟값의 개수 및 안정성, 안장점의 존재 여부 등을 파악할 수 있습니다.
- 예: Gur-Ari et al., 2018 에서는 신경망 손실 표면의 persistence diagram을 계산하여, 넓은(wide) 네트워크가 좁은(narrow) 네트워크보다 더 단순한 위상적 구조를 갖는다는 것을 보였습니다.
일반화 성능 예측: Persistence diagram의 특징(예: 가장 긴 수명을 갖는 0차 특징의 수명)이 모델의 일반화 성능과 상관관계가 있을 수 있습니다.
- 예: Perez et al., 2022는](https://www.google.com/search?q=https://www.google.com/search%3Fq%3Dhttps://proceedings.mlr.press/v162/perez22a.html)%EB%8A%94%EB%8A%94)) persistence diagram의 특징을 사용하여 모델의 일반화 성능을 예측하는 방법을 제안했습니다.
Mode Connectivity: 서로 다른 local minimum을 연결하는 경로를 찾고, 그 경로상의 에너지 장벽(energy barrier)을 분석합니다.
- 예: Garipov et al., 2018

참고 자료:

Edelsbrunner, H., & Harer, J. (2010). Computational Topology: An Introduction. American Mathematical Society.
Gur-Ari, G., Roberts, D. A., & Dyer, E. (2018). Gradient descent happens in a tiny subspace. arXiv preprint arXiv:1812.04754.
Perez, D., Masoomi, A., DiCecco, J., & Chwialkowski, K. (2022). Relating loss landscape topology to generalization with persistent homology. In International Conference on Machine Learning (pp. 17953-17977). PMLR.
Garipov, T., Izmailov, P., Podoprikhin, D., Vetrov, D. P., & Wilson, A. G. (2018). Loss surfaces, mode connectivity, and fast ensembling of dnns. Advances in neural information processing systems, 31.

클릭하여 내용 보기 (딥다이브: 다중 스케일 손실 표면 분석)

다중 스케일 손실 표면 분석

딥러닝 모델의 손실 표면은 다양한 스케일의 특징을 갖습니다. 큰 규모의 계곡(valley)과 능선(ridge)부터 작은 규모의 요철(bump)과 구덩이(hole)까지, 다양한 크기의 기하학적 구조가 학습 과정에 영향을 미칩니다. 다중 스케일 분석은 이러한 다양한 스케일의 특징을 분리하여 분석하는 방법입니다.

핵심 아이디어:

웨이블릿 변환 (Wavelet Transform): 웨이블릿 변환은 신호(signal)를 다양한 주파수(frequency) 성분으로 분해하는 수학적 도구입니다. 이를 손실 함수에 적용하면, 서로 다른 스케일의 특징을 분리할 수 있습니다.
- 연속 웨이블릿 변환 (Continuous Wavelet Transform, CWT):
  
  \(W(a, b) = \int\_{-\infty}^{\infty} f(x) \psi\_{a,b}(x) dx\)
  - \(f(x)\): 분석 대상 함수 (손실 함수)
  - \(\psi\_{a,b}(x) = \frac{1}{\sqrt{a}}\psi(\frac{x-b}{a})\): 웨이블릿 함수 (mother wavelet \(\psi\)를 스케일링(\(a\)) 및 이동(\(b\))시킨 함수)
  - \(W(a, b)\): 스케일 \(a\), 위치 \(b\)에서의 웨이블릿 계수
- Mother Wavelet: 특정 조건을 만족하는 함수 (예: Mexican hat wavelet, Morlet wavelet) (자세한 내용은 참고 문헌 [2] 참조)
다중 해상도 분석 (Multi-resolution Analysis, MRA): CWT를 이산화(discretization)하여, 신호를 서로 다른 해상도(resolution) 레벨로 분해하는 방법입니다.

수학적 배경 (간략):

Scaling Function: 저주파 성분을 나타내는 함수입니다.
Wavelet Function: 고주파 성분을 나타내는 함수입니다.
Decomposition: 신호를 scaling function과 wavelet function의 조합으로 분해합니다.
Reconstruction: 분해된 신호를 다시 원래 신호로 복원합니다. (자세한 내용은 참고 문헌 [1] 참조)

딥러닝 연구 적용:

손실 표면 거칠기 분석: 웨이블릿 변환을 통해 손실 표면의 거칠기(roughness)를 정량화하고, 이것이 학습 속도 및 일반화 성능에 미치는 영향을 분석할 수 있습니다.
- 예: Li et al., 2019는](https://www.google.com/search?q=https://www.google.com/search%3Fq%3Dhttps://arxiv.org/abs/1910.00779)%EB%8A%94%EB%8A%94)) 웨이블릿 기반 다중 해상도 분석을 사용하여 손실 표면의 거칠기가 학습 역학에 미치는 영향을 분석했습니다.
최적화 알고리즘 분석: 최적화 알고리즘이 각 스케일에서 어떤 특징을 따라 이동하는지 분석하여, 알고리즘의 동작 방식을 더 잘 이해할 수 있습니다.

참고 자료:

Mallat, S. (2008). A wavelet tour of signal processing: the sparse way. Academic press.
Daubechies, I. (1992). Ten lectures on wavelets. Society for industrial and applied mathematics.
Li, Y., Hu, W., Zhang, Y., & Gu, Q. (2019). Multiresolution analysis of the loss landscape of deep nets. arXiv preprint arXiv:1910.00779.

5.4 최적화 과정 시각화: 가우시안 함수로 엿보는 딥러닝 학습의 비밀

딥러닝 모델의 실제 손실 표면(loss surface)은 수백만에서 수십억 차원에 이르는 초고차원 공간에 존재하며, 매우 복잡한 기하학적 구조를 가집니다. 따라서 이를 직접 시각화하고 분석하는 것은 사실상 불가능합니다. 또한, 실제 손실 표면은 미분 불가능한 지점, 불연속점, 수치적 불안정성 등 다양한 문제점을 안고 있어, 이론적인 분석에도 어려움이 따릅니다.

5.4.1 가우시안 함수를 통한 근사적 분석: 단순함 속에 숨겨진 통찰

이러한 한계를 극복하고 최적화 과정을 개념적으로 이해하기 위해, 우리는 매끄럽고(smooth), 연속적(continuous)이며, 볼록(convex)한 형태를 갖는 가우시안 함수(Gaussian function)를 사용하여 손실 표면을 근사(approximation)하는 방법을 사용합니다.

가우시안 함수를 사용하는 이유 (손실 표면 근사의 장점):

미분 가능성: 가우시안 함수는 모든 지점에서 무한 번 미분 가능(infinitely differentiable)합니다. 이는 경사 하강법(gradient descent) 기반 최적화 알고리즘을 적용하고 분석하는 데 필수적인 조건입니다.
볼록성(Convexity): 단일 가우시안 함수는 볼록 함수(convex function)입니다. 볼록 함수는 전역 최솟값(global minimum)이 하나만 존재하므로, 최적화 알고리즘의 수렴성을 분석하기 용이합니다.
대칭성(Symmetry): 가우시안 함수는 중심점을 기준으로 대칭적인 형태를 가집니다. 이는 손실 표면의 특정 방향에 대한 편향(bias)이 없음을 의미하며, 최적화 알고리즘의 동작을 분석할 때 단순화된 가정을 할 수 있게 해줍니다.
수학적 단순성: 가우시안 함수는 비교적 간단한 수식으로 표현되므로, 수학적 분석이 용이합니다. 이를 통해 최적화 알고리즘의 동작 원리를 이론적으로 이해하고, 예측 가능한 결과를 도출할 수 있습니다.
조절 가능한 복잡성: 가우시안 혼합 모델을 사용해서 복잡도를 조절할 수 있습니다.

가우시안 함수 수식:

\(z = A \exp\left(-\left(\frac{(x-x_0)^2}{2\sigma_1^2} + \frac{(y-y_0)^2}{2\sigma_2^2}\right)\right)\)

\(A\): 진폭 (amplitude) - 손실 함수의 최대 높이
\(x_0\), \(y_0\): 중심점 (center) - 손실 함수의 최솟값 위치
\(\sigma_1\), \(\sigma_2\): x축, y축 방향의 표준편차 (standard deviation) - 손실 표면의 폭 (넓고 좁음)

물론, 실제 손실 표면은 가우시안 함수보다 훨씬 복잡한 형태를 가질 수 있습니다. (다수의 local minima, saddle point, plateau 등). 하지만, 단일 가우시안 함수를 사용한 근사는 최적화 알고리즘의 기본적인 동작 특성(예: 수렴 속도, 진동 패턴)을 이해하고, 서로 다른 알고리즘을 비교 분석하는 데 유용한 출발점을 제공합니다. 더 복잡한 손실 표면을 모사(simulate)하기 위해서는 여러 개의 가우시안 함수를 조합한 가우시안 혼합 모델(Gaussian Mixture Model, GMM)을 사용할 수 있습니다.

이 절에서는 단일 가우시안 함수를 사용하여 손실 표면을 근사하고, 다양한 최적화 알고리즘(SGD, Adam 등)을 적용하여 학습 궤적(learning trajectory)을 시각화함으로써, 각 알고리즘의 동적 특성과 장단점을 직관적으로 파악해 볼 것입니다.

Code

import torch
import numpy as np
import torch.nn as nn
from torch.utils.data import DataLoader, Subset
from dldna.chapter_05.visualization.loss_surface import hessian_eigenvectors, xy_perturb_loss, visualize_loss_surface, linear_interpolation
from dldna.chapter_04.utils.data import get_dataset  
from dldna.chapter_04.utils.metrics import load_model  
from dldna.chapter_05.optimizers.basic import SGD, Adam
from dldna.chapter_05.visualization.gaussian_loss_surface import (
    get_opt_params,  visualize_gaussian_fit, train_loss_surface, visualize_optimization_path
)


# Device configuration
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# Get the dataset
_, test_dataset = get_dataset(dataset="FashionMNIST")
# Create a small dataset
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)
loss_func = nn.CrossEntropyLoss()

trained_model, _ = load_model(model_file="SimpleNetwork-ReLU.pth", path="tmp/models/")
# trained_model, _ = load_model(model_file="SimpleNetwork-Tanh.pth", path="tmp/models/")

trained_model = trained_model.to(device)

# Loss surface data generation
top_n = 2
top_eigenvalues, top_eignevectors = hessian_eigenvectors(
    model=trained_model,
    loss_func=loss_func,
    data_loader=data_loader,
    top_n=top_n,
    is_cuda=True
)

# Define lambda range
d_min, d_max, d_num = -1, 1, 30
lambda1 = np.linspace(d_min, d_max, d_num).astype(np.float32)
lambda2 = np.linspace(d_min, d_max, d_num).astype(np.float32)

# Calculate loss surface
x, y, z = xy_perturb_loss(
    model=trained_model,
    top_eigenvectors=top_eignevectors,
    data_loader=data_loader,
    loss_func=loss_func,
    lambda1=lambda1,
    lambda2=lambda2,
    device=device
)


# After generating loss surface data
popt, _, offset = get_opt_params(x, y, z)

# Visualize Gaussian fitting
visualize_gaussian_fit(x, y, z, popt, offset, d_min, d_max, d_num)

# View from a different angle
visualize_gaussian_fit(x, y, z, popt, offset, d_min, d_max, d_num,
                      elev=30, azim=45)

Function parameters = [29.27164346 -0.0488573  -0.06687705  0.7469189   0.94904458]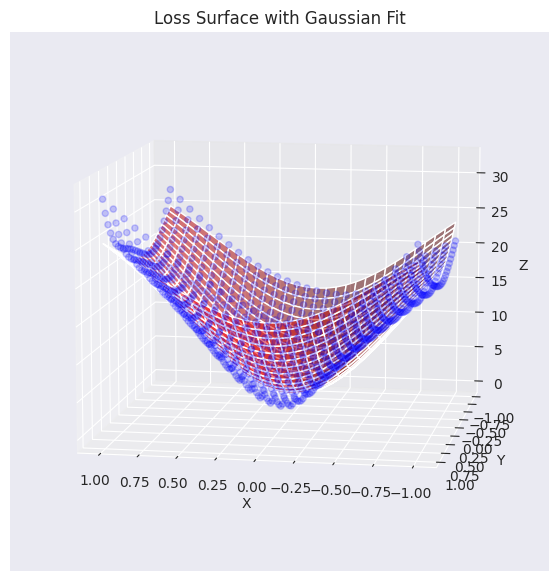

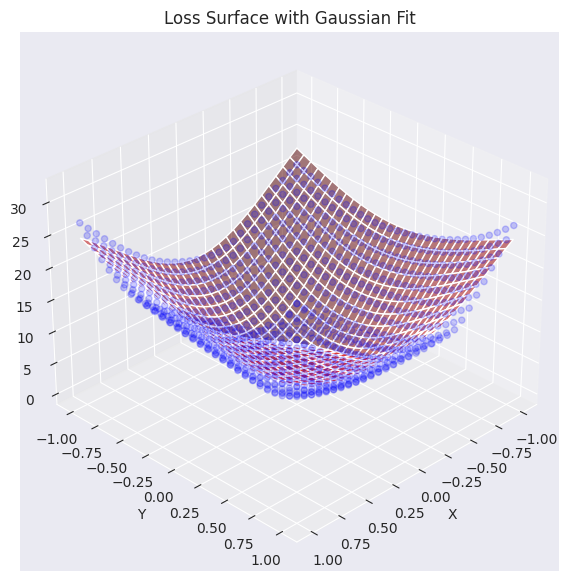
실제 손실 평면 데이터(파란 점)와 가우시안 함수로 근사한 평면(붉은색)을 겹쳐서 시각화했습니다. 그래프에서 볼 수 있듯이, 생성된 가우시안 함수가 원래 손실 표면 데이터의 전반적인 경향(특히, 중심부의 오목한 형태)을 비교적 잘 포착하여, 유사한 곡면을 생성하고 있습니다. 이제 이 근사된 손실 평면 함수를 이용하여, 다양한 최적화 알고리즘(optimizer)이 어떻게 최솟값을 찾아가는지 그 경로를 분석하고 시각화할 것입니다.

5.4.2 경로 시각화

가우시안 함수로 근사한 손실평면을 사용하여, 옵티마이저가 어떻게 작동하는 2D 평면에서 시각화 해보겠습니다.

Code

# Gaussian fitting
popt, _, offset = get_opt_params(x, y, z)
gaussian_params = (*popt, offset)

# Calculate optimization paths
points_sgd = train_loss_surface(
    lambda params: SGD(params, lr=0.1),
    [d_min, d_max], 100, gaussian_params
)
points_sgd_m = train_loss_surface(
    lambda params: SGD(params, lr=0.05, momentum=0.8),
    [d_min, d_max], 100, gaussian_params
)
points_adam = train_loss_surface(
    lambda params: Adam(params, lr=0.1),
    [d_min, d_max], 100, gaussian_params
)

# Visualization
visualize_optimization_path(
    x, y, z, popt, offset,
    [points_sgd, points_sgd_m, points_adam],
    act_name="ReLU"
)

그래프는 가우시안 함수로 근사된 손실 표면에서 SGD, Momentum SGD, Adam 세 가지 최적화 알고리즘의 학습 경로를 보여줍니다. 경사가 완만한 영역과 급한 영역 모두에서 세 알고리즘은 각기 다른 특성을 보입니다.

SGD (주황색): 경사가 완만한 곳에서는 비교적 넓은 폭으로 진동하며 최저점을 향해 나아가지만, 경사가 급한 곳에서는 더욱 큰 폭으로 진동하며, 최저점 근처에서 수렴 속도가 느려지는 경향을 보입니다.
Momentum SGD (초록색): SGD보다 진동이 덜하고, 더 부드러운 곡선 형태로 최저점에 접근합니다. 관성(momentum) 효과 덕분에 경사가 급한 영역에서도 비교적 안정적으로 최저점을 찾아갑니다.
Adam (빨간색): 가장 적은 진동으로, 경사 변화에 민감하게 반응하며 효율적인 경로를 따라 최저점에 도달합니다. 특히, 경사가 급한 영역에서도 상대적으로 빠른 수렴 속도를 보입니다. 이는 Adam의 적응형 학습률(adaptive learning rate) 조정 메커니즘 덕분입니다.

실무에서는 SGD 자체보다는 모멘텀을 적용한 SGD가 훨씬 선호되며, Adam 또는 AdamW와 같은 적응형 최적화 알고리즘도 널리 사용됩니다. 일반적으로 손실 표면은 대부분의 영역에서 평탄(flat)하지만, 최솟값 근처에서는 좁고 깊은 골짜기(narrow valley) 형태를 띠는 경향이 있습니다. 이로 인해 큰 학습률(learning rate)은 최솟값을 지나치거나(overshoot) 발산(diverge)할 위험이 있으므로, 학습률을 점진적으로 감소시키는 학습률 스케줄러(learning rate scheduler)를 함께 사용하는 것이 일반적입니다. 또한, 최적화 알고리즘의 선택뿐만 아니라, 적절한 학습률 스케줄러, 배치 크기, 정규화 기법 등을 함께 고려하는 것이 중요합니다.

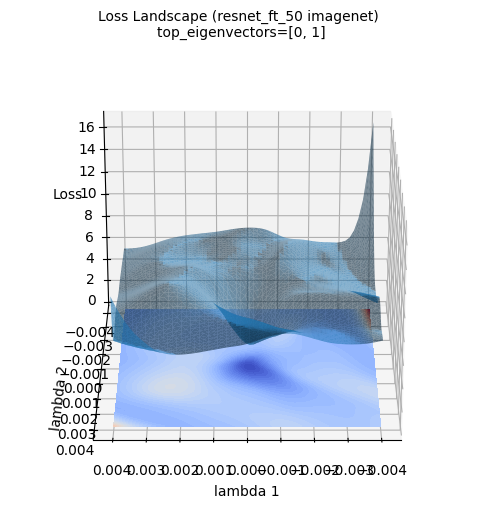
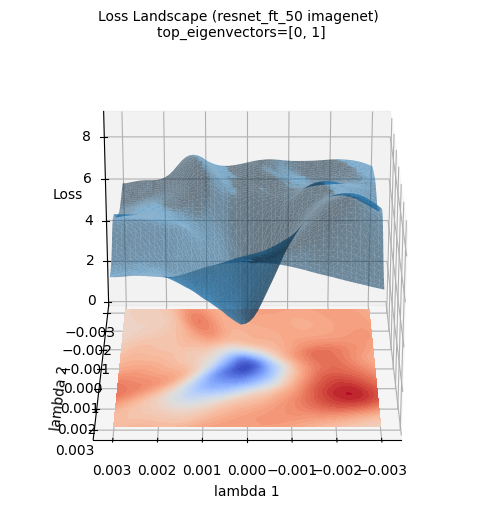
위 손실평면 이미지는 ImageNet 데이터셋으로 신규 학습한 ResNet-50 모델의 손실 표면을 3차원으로 시각화한 것입니다. (PyHessian을 사용하여 계산된 헤시안 행렬의 상위 고유벡터 두 개를 축으로 사용). 가우시안 함수 근사와는 달리, 실제 딥러닝 모델의 손실 표면은 훨씬 더 복잡하고 불규칙한 형태를 띠고 있음을 알 수 있습니다. 그럼에도 중심부(파란색 영역)에 최솟값이 존재한다는 큰 경향은 유지함을 알 수 있습니다. 이러한 시각화는 딥러닝 모델의 실제 손실 표면이 얼마나 복잡한 지형을 갖는지, 그리고 왜 최적화가 어려운 문제인지에 대한 직관적인 이해를 돕습니다.

5.5 최적화 과정의 동적 분석: 학습 궤적의 탐구

딥러닝 모델 학습에서 최적화 알고리즘이 어떤 경로로 손실 함수 최솟값을 찾아가는지, 그 동적 특성(dynamics)을 이해하는 것은 중요합니다. 특히, 대규모 언어 모델(LLM) 등장으로, 수십억 개 파라미터 모델의 학습 동역학 분석 및 제어가 더욱 중요해졌습니다.

5.5.1 훈련 과정의 특징

딥러닝 모델 학습 과정은 초기, 중기, 후기 단계로 나눌 수 있으며, 각 단계별 특징이 있습니다.

학습 단계별 특성:
- 초기: 그래디언트 노름(gradient norm)이 크고 변동이 심하며, 손실 함수 값이 급격히 감소합니다.
- 중기: 그래디언트가 안정화되며, 파라미터는 최적 영역(optimal region)을 탐색(explore)합니다.
- 후기: 파라미터는 지역 최적해(local optimum) 주변에서 미세 조정(fine-tuning)됩니다. (조기 종료 중요)
층별 그래디언트 특성:
- 깊은 신경망에서는 입력층에 가까울수록 그래디언트가 크고, 출력층에 가까울수록 작아지는 경향이 있습니다. (vanishing gradient problem)
- 이는 역전파(backpropagation) 시 연쇄 법칙(chain rule) 때문입니다.
- 잔차 연결(residual connection)은 이러한 불균형을 완화하여 깊은 층에서도 안정적 학습을 돕습니다.
파라미터 의존성:
- 신경망 파라미터들은 상호 의존적이며, 이는 최적화 과정을 비선형적(nonlinear)으로 만듭니다.
- 일부 파라미터가 학습에 더 큰 영향을 미칠 수 있으므로, 파라미터 간 균형(balance)이 중요합니다.
최적화 경로 분석:
- 최적화 과정에서 파라미터가 손실 표면 위를 이동하는 경로를 최적화 경로(optimization path)라고 합니다.
- 넓고 완만한 계곡(valley) 형태의 지역 최솟값이 좁고 뾰족한 계곡보다 일반화 성능(generalization performance)이 좋은 경향이 있습니다.
- 고차원 공간에서는 안장점(saddle point)이 매우 흔합니다. (모멘텀, Adam 등이 회피하도록 설계)
- 손실 표면이 평탄한(flat) 영역에서는 그래디언트가 작아져 학습이 느려질 수 있습니다. (적응형 학습률 알고리즘이 도움)

5.5.2 학습 안정성 분석 및 제어

안정성 분석 방법론

최적화 과정의 안정성(stability) 분석을 위해 다음을 고려합니다.

그래디언트 진단 (Gradient Diagnostics):
- 그래디언트 소실(vanishing gradient) 또는 폭발(exploding gradient) 현상 감지.
- 훈련 과정에서 그래디언트 노름(norm)을 주기적으로 관찰.
헤시안 기반 분석 (Hessian-based Analysis):
- 헤시안(Hessian) 행렬의 고윳값(eigenvalue) 분포와 조건수(condition number)는 최적화 경로 안정성을 나타냅니다.
- (5.3절의 헤시안 기반 시각화 참고)
실시간 모니터링 (Real-time Monitoring):
- 학습 중 그래디언트 노름, 파라미터 업데이트 크기, 손실 함수 값, 성능 지표 등을 실시간 모니터링.

안정화 기법 (Stabilization Techniques)

그래디언트 클리핑 (Gradient Clipping): 그래디언트 크기(norm)가 임계값(threshold)을 넘지 않도록 제한.

\(g \leftarrow \text{clip}(g) = \min(\max(g, -c), c)\)
- \(g\): 그래디언트, \(c\): 임계값
적응형 학습률 (Adaptive Learning Rate): Adam, RMSProp, Lion, Sophia 등은 그래디언트 통계에 따라 학습률 자동 조절.
학습률 스케줄러 (Learning Rate Scheduler): 학습 에폭(epoch) 또는 검증 손실(validation loss)에 따라 학습률 점진적 감소.
하이퍼파라미터 최적화 (Hyperparameter Optimization): 최적화 관련 하이퍼파라미터를 자동 탐색/조정.

맺음말

이번 5장에서는 딥러닝 모델 학습의 핵심 요소인 최적화와 관련된 다양한 주제들을 깊이 있게 살펴보았습니다. 가중치 초기화 방법의 중요성, 다양한 최적화 알고리즘(SGD, Momentum, Adam, Lion, Sophia, AdaFactor)의 원리와 특성, 그리고 손실 표면 시각화 및 학습 동역학 분석을 통해 딥러닝 모델의 학습 과정을 더 잘 이해할 수 있게 되었습니다.

6장에서는 딥러닝 모델의 일반화 성능을 향상시키기 위한 핵심 기법인 규제(regularization)에 대해 자세히 알아봅니다. L1/L2 규제, 드롭아웃(dropout), 배치 정규화(batch normalization), 데이터 증강(data augmentation) 등 다양한 규제 기법의 원리와 효과를 살펴보고, 실전 예제를 통해 그 적용 방법을 익힐 것입니다.

연습 문제

기본 문제

SGD 수동 계산: 학습률이 0.1이고 모멘텀이 0.9일 때, 다음 손실 함수 \(L(w) = w^2\) 에 대한 SGD 업데이트 규칙을 3단계 이상 수동으로 계산해보세요. 초기 가중치는 \(w_0 = 2\)로 설정합니다.
경사하강법 수렴 속도 비교: 간단한 2차원 함수 \(f(x, y) = x^2 + 2y^2\) 에 대해 경사하강법을 적용하고, 학습률을 0.1, 0.01, 0.001로 변경하면서 수렴 속도를 비교해보세요.
초기화 방법 비교: Kaiming 초기화와 Xavier 초기화를 비교하고, ReLU 활성화 함수와 함께 사용할 때 Kaiming 초기화가 더 적합한 이유를 설명해보세요.

응용 문제

Adam 옵티마이저: Adam 옵티마이저의 작동 원리를 (수식을 포함하여) 설명하고, \(\beta_1\) 과 \(\beta_2\) 파라미터의 역할에 대해 설명해보세요.
배치 정규화와 초기화: 배치 정규화(Batch Normalization)가 초기화 방법의 중요성을 어떻게 감소시키는지 설명하고, 그 이유를 설명해보세요.
가우시안 손실 평면: 가우시안 함수를 사용해서 손실 평면을 근사하는 예제(5.5.1절)에서, 가우시안 함수의 파라미터(진폭, 중심점, 분산)가 최적화 과정에 미치는 영향에 대하여 설명해보세요. (각 파라미터를 변경하면서 최적화 경로가 어떻게 달라지는지 관찰해보세요.)

심화 문제

Lion 옵티마이저 분석: Lion 옵티마이저의 핵심 아이디어를 (수식을 포함하여) 설명하고, Adam과 비교하여 어떤 장단점이 있는지 분석해보세요.
초기화 방법 실험: 주어진 데이터셋(예: FashionMNIST)과 모델(5.1절의 SimpleNetwork)에 대해, 서로 다른 초기화 방법(LeCun, Xavier, Kaiming, Orthogonal)을 적용하여 학습시키고, 그 결과(오차율, 수렴 속도, 평균 조건수, 스펙트럴 놈, 유효 랭크비)를 비교 분석해보세요.
최적화 경로 시각화: 5.5절의 최적화 경로 시각화 코드를 참고하여, 자신만의 손실 함수(예: 다봉형 함수, 비볼록 함수)를 정의하고, 다양한 옵티마이저(SGD, Momentum, Adam, Lion 등)의 최적화 경로를 시각화하고 비교 분석해보세요. (최소 3개 이상의 옵티마이저 비교)

클릭하여 내용 보기 (위상 기반 손실 표면 분석)

연습 문제 해답

기본 문제

SGD 수동 계산:
- 1단계:
  - \(g_0 = \frac{dL}{dw}(w_0) = 2w_0 = 4\)
  - \(v_0 = 0\) (모멘텀 초기값)
  - \(w_1 = w_0 - \eta v_1 = 2 - 0.1 \cdot (0.9 \cdot 0 + 4) = 1.6\)
- 2단계:
  - \(g_1 = 2w_1 = 3.2\)
  - \(v_1 = 0.9 \cdot v_0 + g_0= 0.9 \cdot 0 + 4 = 4\)
  - \(w_2 = w_1 - \eta \cdot (0.9 \cdot v_1 + g_1) = 1.6 - 0.1 \cdot (0.9 \cdot 4+ 3.2) = 0.92\)
- 3단계:
  - \(g_2 = 2w_2 = 1.84\)
  - \(v_2 = 0.9 \cdot 4 + 3.2 = 6.8\)
  - \(w_3 = w_2 - \eta \cdot (0.9 * v_2 + g_2) = 0.92 - 0.1 \cdot (0.9 \cdot 6.8 + 1.84) = 0.124\)
경사하강법 수렴 속도 비교:
- 학습률이 클수록 (0.1) 초기 수렴은 빠르지만, 최적점 근처에서 진동할 수 있습니다.
- 학습률이 작을수록 (0.001) 수렴 속도는 느리지만, 더 안정적으로 최적점에 접근합니다.
- 적절한 학습률(0.01)은 적당한 수렴속도와 안정성을 보입니다.
초기화 방법 비교:
- Kaiming 초기화: ReLU 활성화 함수의 특성(음수 입력을 0으로 만듦)을 고려하여, \(\sqrt{2/n_{in}}\) 의 표준편차를 갖는 분포로 가중치를 초기화합니다.
- Xavier 초기화: 활성화 함수의 종류와 관계없이 입력과 출력의 분산을 유지하는 \(\sqrt{2/(n_{in} + n_{out})}\) 의 표준편차를 사용합니다.
- ReLU + Kaiming: ReLU는 양수 영역에서 선형 활성화를 가지므로, Kaiming 초기화가 더 큰 분산을 제공하여 “죽은 뉴런” 문제를 완화하고, 더 빠른 학습을 돕습니다.

응용 문제

Adam 옵티마이저:
- 작동 원리: Adam은 모멘텀(Momentum)과 RMSProp의 아이디어를 결합한 옵티마이저입니다.
  - 모멘텀: 과거 그래디언트의 지수 가중 평균(1차 모멘트, \(m_t\))을 사용하여 관성을 부여합니다.
  - RMSProp: 과거 그래디언트 제곱의 지수 가중 평균(2차 모멘트, \(v_t\))을 사용하여 파라미터별 학습률을 조정합니다.
  - 편향 보정: 초기 단계에서 \(m_t\) 와 \(v_t\) 가 0으로 편향되는 것을 보정합니다.
- 수식:
  - \(m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t\)
  - \(v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2\)
  - \(\hat{m_t} = m_t / (1 - \beta_1^t)\)
  - \(\hat{v_t} = v_t / (1 - \beta_2^t)\)
  - \(w_{t+1} = w_t - \eta \hat{m_t} / (\sqrt{\hat{v_t}} + \epsilon)\)
- \(\beta_1\), \(\beta_2\) 역할:
  - \(\beta_1\): 1차 모멘트(모멘텀)의 지수 감소율을 조절합니다. (일반적으로 0.9)
  - \(\beta_2\): 2차 모멘트(RMSProp)의 지수 감소율을 조절합니다. (일반적으로 0.999)
배치 정규화와 초기화:
- 배치 정규화: 각 미니배치의 입력을 평균 0, 분산 1로 정규화합니다.
- 초기화 중요성 감소: 배치 정규화는 네트워크 내부 공변량 변화(internal covariate shift)를 줄여, 초기 가중치 분포에 대한 의존성을 낮춥니다.
- 이유: 정규화된 입력은 활성화 함수를 적절한 범위(예: ReLU의 양수 영역)에 위치시켜, 그래디언트 소실/폭발 문제를 완화하고, 학습을 안정화합니다.
가우시안 손실 평면:
- 진폭 (A): 손실 함수의 전반적인 크기를 조절합니다. 진폭이 크면 손실 값의 변화폭이 커져 학습이 불안정해질 수 있습니다.
- 중심점 (\(x_0\), \(y_0\)): 손실 함수의 최솟값 위치를 결정합니다. 최적화 알고리즘은 이 중심점을 향해 이동합니다.
- 분산 (\(\sigma_1\), \(\sigma_2\)): 각 축 방향으로의 손실 함수 변화 정도를 나타냅니다. 분산이 작으면 좁고 뾰족한 형태, 크면 넓고 완만한 형태가 됩니다. 분산이 다르면 각 방향으로의 학습 속도를 다르게 조절해야 합니다.

심화 문제

Lion 옵티마이저 분석:
- 핵심 아이디어: 그래디언트의 부호(sign)만을 사용하여 업데이트를 수행합니다.
- 수식: c_t = β_1 * m_{t-1} + (1 - β_1) * g_t w_{t+1} = w_t - η * sign(c_t) m_t = c_t
  - update의 부호만 사용하므로, Adam처럼 2nd moment를 계산, 저장할 필요없음
- 장점:
  - Adam보다 메모리 사용량이 적습니다. (2차 모멘트를 저장하지 않음)
  - 업데이트 크기가 모든 파라미터에 대해 동일하여, 희소한 그래디언트에 강건합니다.
- 단점:
  - 그래디언트의 크기 정보를 무시하므로, 특정 상황에서 Adam보다 느리게 수렴할 수 있습니다.
  - 학습률 튜닝이 Adam보다 더 민감할 수 있습니다.
초기화 방법 실험:
- 실험 설계:
  - 동일한 모델(SimpleNetwork)과 데이터셋(FashionMNIST)을 사용합니다.
  - LeCun, Xavier, Kaiming, Orthogonal 초기화를 각각 적용합니다.
  - 동일한 최적화 알고리즘(예: Adam)과 학습률을 사용합니다.
  - 충분한 에폭(예: 20) 동안 학습시키고, 각 에폭마다 평가 지표(오차율, 수렴 속도, 평균 조건수, 스펙트럴 놈, 유효 랭크비)를 기록합니다.
- 결과 분석:
  - ReLU 활성화 함수를 사용하는 경우, Kaiming 초기화가 가장 좋은 성능을 보일 가능성이 높습니다.
  - Orthogonal 초기화는 RNN/LSTM에서 좋은 성능을 보일 수 있습니다.
  - Xavier 초기화는 tanh, sigmoid 활성화 함수에서 좋은 성능을 보일 수 있습니다.
  - LeCun 초기화는 현대적인 네트워크에서는 성능이 떨어질 수 있습니다.
최적화 경로 시각화:
- 자신만의 손실 함수 정의:
  - 예: \(f(x, y) = (x^2 + y - 11)^2 + (x + y^2 - 7)^2\) (Himmelblau 함수, 다봉형 함수)
  - 예: \(f(x, y) = 0.5x^2 - 0.25y^2 + 3\) (안장점(saddle point)이 있는 비볼록 함수)
- 최적화 알고리즘 선택: SGD, Momentum(SGD with momentum), Adam, Lion
- 시각화: 5.5절의 코드를 참고하여 각 옵티마이저의 최적화 경로를 2차원 평면에 시각화합니다.
- 결과 분석:
  - SGD는 지역 최솟값/안장점에 빠질 가능성이 높습니다.
  - Momentum은 관성을 통해 지역 최솟값을 탈출할 가능성이 있지만, 진동할 수 있습니다.
  - Adam은 적응형 학습률 덕분에 더 효율적으로 최적점에 도달할 수 있습니다.
  - Lion은 Adam과 유사하거나 더 빠른 수렴을 보일 수 있지만, 학습률 튜닝에 민감할 수 있습니다.
  - 다봉, 안장점 등 손실함수의 형태에 따라 최적화 결과를 비교분석합니다.

참고 자료

An overview of gradient descent optimization algorithms (Sebastian Ruder, 2016) - 딥러닝 최적화 알고리즘에 대한 훌륭한 개요 논문입니다. SGD, Momentum, AdaGrad, RMSProp, Adam 등 다양한 알고리즘을 비교 분석합니다.
Visualizing the Loss Landscape of Neural Nets (Li et al., 2018) - 손실 표면 시각화에 대한 선구적인 논문입니다. 잔차 연결(residual connection)이 손실 표면을 어떻게 평탄화하는지 보여줍니다.
Optimization for Deep Learning Highlights in 2023 (Sebastian Ruder, 2023) - 2023년 딥러닝 최적화 주요 내용을 요약한 블로그 글입니다. 최신 연구 동향을 파악하는 데 유용합니다.
Improving Deep Learning with Better Initialization (Mishkin & Matas, 2021) - 초기화에 대한 현대적 연구 동향을 담은 논문입니다. 다양한 초기화 방법을 비교하고, 실용적인 가이드라인을 제시합니다.
Symbolic Discovery of Optimization Algorithms (Chen et al. 2023) - 구글 브레인에서 발견한 Lion 알고리즘에 관한 논문
PyHessian: Neural Networks Through the Lens of the Hessian (Yao et al., 2020) - 헤시안 행렬을 이용한 손실 표면 분석 도구 PyHessian에 대한 논문입니다.
The Marginal Value of Adaptive Gradient Methods in Machine Learning (Wilson et al., 2017) - 적응형 학습률 방법(Adam 등)이 항상 SGD보다 좋은 것은 아니라는 것을 보여주는 논문입니다.
How to escape saddle points efficiently (Ge et al., 2015) - 섭동 경사하강법(perturbed gradient descent)을 사용하여 안장점을 효율적으로 탈출하는 방법을 설명하는 블로그 글입니다.
Deep Understanding of Modern Initialization Methods with Block Diagonal Matrices (Huang et al., 2021) - 블록 대각 행렬을 사용하여 초기화 방법을 분석하는 논문입니다.
AdaHessian: An Adaptive Second Order Optimizer for Machine Learning (Yao et al., 2020) - 헤시안 행렬의 대각 성분을 사용하여 2차 정보를 활용하는 AdaHessian 옵티마이저에 대한 논문입니다.
A Closer Look at Smoothness in Deep Learning: A Tensor Decomposition Approach (Li et al., 2024) - 텐서 분해를 사용하여 딥러닝 모델의 평활성(smoothness)을 분석하는 논문입니다.
Understanding Measures of Efficiency for Stochastic Optimization (Defazio & Bottou, 2025) - 확률적 최적화 알고리즘의 효율성을 측정하는 방법을 제안하는 논문입니다.
Deep Learning (Goodfellow, Bengio, Courville, 2016) - 딥러닝 교과서. 6장(Deep Feedforward Networks), 8장(Optimization for Training Deep Models)에서 초기화 및 최적화 관련 내용을 다룹니다.
Stanford CS231n: Convolutional Neural Networks for Visual Recognition - 스탠포드 대학교 딥러닝 강의. Optimization 파트에서 최적화 관련 내용을 다룹니다.
Papers with Code - Optimization Methods - 최적화 관련 최신 논문들을 모아놓은 웹사이트입니다.

5. 최적화와 시각화

5.1 파라미터 초기화의 발전과 현대적 접근

5.1.1 초기화 방법의 수학적 원리

전통적 초기화

현대적 초기화

최신 초기화 (2023년 이후)

수학적 원리

심층 신경망 초기화의 수학적 원리와 최신 기법

1. 분산 보존 원리 (Variance Preservation Principle)

1.1 이론적 기반

1.2 비선형 활성화 함수 확장

1.3 확률론적 접근 (참고)

2. 스펙트럴 제어 (Spectral Control)

2.1 특이값 분해와 학습 역학

2.2 동적 스펙트럴 정규화

3. 표현력 최적화 (Expressivity Optimization)

3.1 유효 랭크 이론

3.2 초기화 전략 비교표

3.3 Emergence-Promoting 초기화

4. 초기화와 최적화의 상호작용

4.1 NTK 이론 확장

4.2 메타 초기화 전략

5. (참고) 물리 기반 초기화 기법

6. 실용적 권장 사항

참고 문헌

5.1.2 초기화 방법: 실전 비교 분석

5.1.3 실무적 권장사항 및 추가 고려 사항

기본 원칙

모델 규모 및 특성

추가 고려 사항

5.2 최적화 알고리즘: 딥러닝 학습의 핵심 엔진

5.2.1 최적화 알고리즘의 발전과 구현 - 계속되는 진화

최적화 알고리즘의 역사

기본 최적화 알고리즘

현대적 최적화 알고리즘: 더 빠르고, 더 효율적으로, 더 큰 모델을 위해

현대 최적화 알고리즘의 심층 분석

Lion (EvoLved Sign Momentum)

Sophia (Second-order Clipped Stochastic Optimization)

AdaFactor

그 외 참고할 만한 최신 최적화 알고리즘

5.2.2 최적화 훈련 비교

기본 태스크 분석

고급 태스크 평가

5.3 최적화 과정의 시각화와 분석: 딥러닝 학습의 블랙박스 들여다보기

5.3.1 손실 표면(Loss Landscape)의 이해: 딥러닝 모델의 지형도

기본 시각화 기법

5.3.2 손실 표면 분석의 심층 기법

위상 기반 손실 표면 분석

다중 스케일 손실 표면 분석

5.4 최적화 과정 시각화: 가우시안 함수로 엿보는 딥러닝 학습의 비밀

5.4.1 가우시안 함수를 통한 근사적 분석: 단순함 속에 숨겨진 통찰

5.4.2 경로 시각화

5.5 최적화 과정의 동적 분석: 학습 궤적의 탐구

5.5.1 훈련 과정의 특징

5.5.2 학습 안정성 분석 및 제어

안정성 분석 방법론

안정화 기법 (Stabilization Techniques)

최신 연구 동향

맺음말

연습 문제

기본 문제

응용 문제

심화 문제

연습 문제 해답

기본 문제

응용 문제

심화 문제

참고 자료